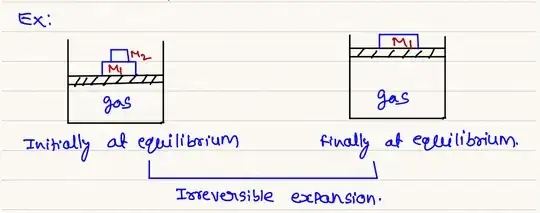
The equilibrium position with $M_1$ only is different from that when we have $M_1+M_2$. Even if we have oscillations around this new equilibrium position, we are never really returning to the initial state, where $M_2$ was also on the top.
Then the claim that the system would perform oscillations is based on a few assumptions that do not hold, if we analyze the physics of the processes more carefully (the list is not comprehensive):
- The force is not proportional to displacement, but rather to the inverse of it: $$PV=nkT\Rightarrow F\propto P \propto \frac{1}{V}\propto \frac{1}{l}$$
- Secondly, there will be energy transfer from the piston to the gas, which may serve as damping
Update
Isentropic description
To pinpoint the flaw in the argument presented in the Q., I will try to formulate it mathematically. If the expansion of the gas is adiabatic and isentropic, the pressure and volume are related via the Laplace law (not sure it is called this way in English though):
$$
PV^\gamma=\text{const}
$$
For convenience, let us measure the position from the bottom of the container, so that the volume is given by $V=Ax$, where $A$ is the cross-sectional area. Then, the force on the container due to the gas is
$$
F_P=PA=\frac{P_0V_0^\gamma}{V^\gamma}A=P_0A\left(\frac{x_0}{x}\right)^\gamma,
$$
and the Newton's second law for the piston is
$$
M_1\ddot{x}(t)=P_0A\left(\frac{x_0}{x}\right)^\gamma-M_1g=-\frac{dU(x)}{dx},
$$
where the potential energy is:
$$
U(x)=M_1 gx +\frac{P_0Ax_0^\gamma}{(\gamma-1)x^{\gamma -1}}.
$$
Since the motion can be described by a potential energy, which has a Unique minimum and goes to infinity for $x\rightarrow 0,+\infty$, we expect oscillations to occur (although non-linear ones), after a period of oscillations, the piston should return to its initial position $x_0$. The equilibrium position for these oscillations (zero net force) is
$$
x_{eq}=x_0\left(\frac{P_0A}{M_1 g}\right)^{\frac{1}{\gamma}}.
$$
Adiabatic $\neq$ isentropic
The invalid assumption here is that the adiabatic expansion is necessarily isentropic, which is not the case (i.e., the Laplace law does not apply.) Indeed, as the piston moves upwards, there are molecules that are moving faster than the piston, and transfer energy to it, and molecules that are moving slower and never catch it. This creates a thermodynamic disequilibrium, which means that gas should equilibrate, thus increasing its entropy. The faster the piston moves, the bigger is the violation of isentropic condition. On the other hand, the slower it moves, the less is the entropy increase, and the process becomes fully isentropic when the motion is infinitely slow... which however contradicts to our assumption that the piston returns to its initial position after a finite oscillation period.
However, provided that the maximum velocity of piston is not very big, the increase of entropy after one oscillations may not be very significant, and many oscillations might happen before the piston stops moving.
Finally, we can find the position at which the piston finally stops. From the force balance we have in the beginning
$$
P_0A=(M_1+M_2)g\Longleftrightarrow P_0V_0=(M_1+M_2)gx_0=nRT_0,
$$
and in the end
$$
P_1A=M_1g\Longleftrightarrow P_1V_1=M_1gx_1=nRT_1,
$$
so that
$$
nR(T_1-T_0)=M_1gx_1 - (M_1+M_2)gx_0.
$$
On the other hand, the energy conservation gives us
$$
\frac{f}{2}nRT_0 + M_1 gx_0=\frac{f}{2}nRT_1+M_1gx_1\Longleftrightarrow nR(T_1-T_0)=\frac{2}{f}M_1(x_0-x_1)
$$
We thus have
$$
\frac{2}{f}M_1(x_0-x_1)=M_1gx_1 - (M_1+M_2)gx_0\Rightarrow\\
x_1=x_0\left(1+\frac{M_2}{M_1\gamma}\right)
$$
($\gamma=(f+2)/f$.)
Comparing this with our earlier expression
$$
x_{eq}=x_0\left(\frac{P_0A}{M_1 g}\right)^{\frac{1}{\gamma}}=
x_0\left(\frac{M_1+M_2}{M_1}\right)^{\frac{1}{\gamma}}\approx
x_0\left(1+\frac{M_2}{M_1\gamma}\right),
$$
where the last equality assumes $M_2\ll M_1$.