19

If you take a piece of paper, keep a finger on its edges and slide both the edges towards the centre, the shape that the side facing you makes looks kind of like a bell-curve. Is it possible to prove that it actually is a bell-curve? If it isn't is there an equation that can model it? I tried this in class when I was bored. I have no background in physics and that is why I can't share my work on this. I had no idea what to put as a tag, so I put newtonian mechanics.

paulina
  • 3,488
Supernerd411
  • 319

1 Answers1

31

This is essentially the shape of the clamped–clamped elastica, which has different origins and a different functional description than the bell curve.

The elastica problem involves an inextensible but easily bendable line/surface and the shape it assumes when the endpoints are held in a certain way.

Broadly, the resulting curvature is such the restoring force from bending (mediated by material's curvature and flexural rigidity) is equal and opposite to the applied bending forces (in this case, arising from your horizontal pushing force and any vertical reaction force from the table).

This is expressed as the nonlinear differential equation

$$B\ddot\theta(s)+P\sin\theta(s)+R\cos\theta(s)=0,$$

with flexural rigidity $B$, angle $\theta(s)$ at a certain normalized distance $s$, pushing force $P$, and reaction force $R$.

The solution is discussed in, for example, Bigoni et al., "New phenomena in nonlinear elastic structures: from tensile buckling to configurational forces":

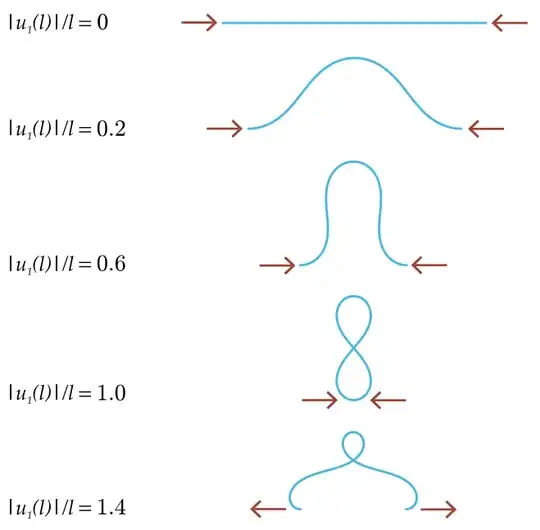
I believe the second shape is approximately the one you observed and are asking about:

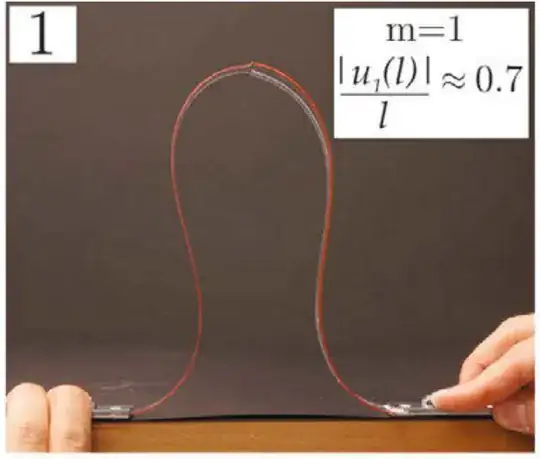
Elastica solutions typically involve elliptic integrals, whereas the bell curve is described (arguably more simply) by an exponential. Symmetry arguments here allow the first mode of the clamped–clamped elastica to be divided into four segments of the pinned–pinned case image source:

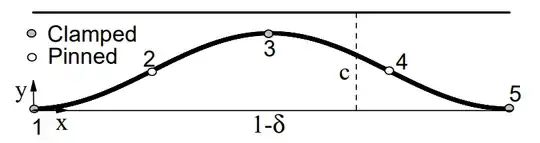
The height $y$ here is $\frac{4p}{\lambda}$, where $\lambda^2=\frac{P}{B}$ and $p$ satisfies the elliptic integral

$$\lambda L=2\int_0^{\pi/2}\frac{d\phi}{\sqrt{1-p^2\sin^2\phi}}$$

with $L$ being the length of the paper between your pushing fingers. Some mechanics texts and handbooks tabulate the corresponding numerical solutions.

For small deflections, the segments assume a sinusoidal shape. The Euler buckling analysis in particular applies this small-deflection assumption.

Chemomechanics
  • 30,163