What can we conclude from Hubble's observation?

Question

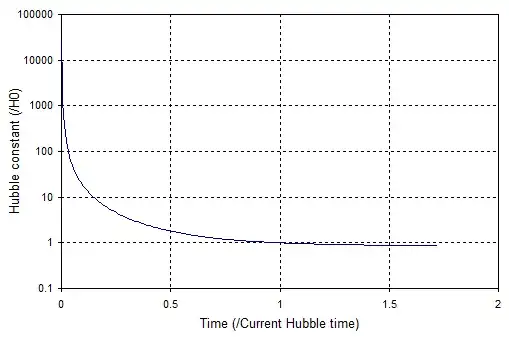
Hubble observed that the further away a galaxy or star is, the greater the redshift observed. So the velocity of the observed galaxies is higher for those that are farther away from us. Now the conclusion I know from the books is that the universe is expanding, and is accelerating.

Now my question is: What if I don't see the redshift as a function of distance? What if I see it as a function of time? Can I say the galaxies were moving faster in the the past, and now they have slowed down. Because, the farther they are from us, the further they are in the past from us! So can I conclude that universe is decelerating with time?

Answer 1

The expansion rate is a function of time and the redshifts of distant galaxies do map out the history of that expansion.

Hubble's original observations of receding galaxies, at distances of millions to tens of millions of light years, revealed that the universe was expanding. However, they did not probe far enough back in time to judge whether that expansion was accelerating or decelerating, because the universe changes on timescales of billions of years.

It was observations of supernovae, at distances of billions of light years, in the 1990s by groups led by Perlmutter, Riess et al. that established the need for the expansion to have accelerated over the last few billion years.

Subsequent observations of even more distant supernovae at distances beyond 5 billion light years are demonstrating that prior to that, the expansion was decelerating.

The "light travel time" effect you are considering, is accounted for in these analyses.

Answer 2

Suppose the Hubble constant $H_0$ was really a constant, then a galaxy at some distance $x$ from us would have a recession velocity of $v=Hx$ regardless of what time we observed the galaxy. It wouldn't matter that as we looked farther out we were seeing backing in time - Hubble's law would still hold.

However the Hubble parameter, $H(t)$, has changed (decreased) since the Big Bang, and assuming dark energy is a simple cosmological constant it will approach a constant value in the future. The Hubble constant $H_0$ is the value of $H(t)$ right now. I calculated the time variation of $H(t)$ in my answer to How does the Hubble parameter change with the age of the universe? and the results are:

This change didn't matter much to Hubble as he could look only at relatively near galaxies so the change in the Hubble parameter was relatively small. However as Rob says in his answer, when we look at very distance galaxies we need to take the change in $H(t)$ into account.

So you are quite correct that we do need to take the different times we see distant galaxies into account, but you can be reassured that cosmologists have thought of this.