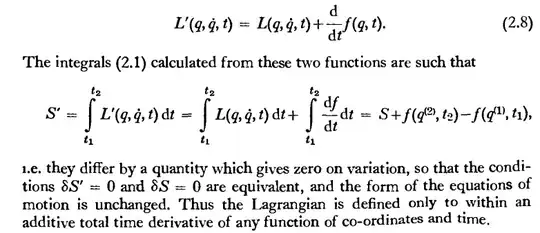0

I was going through Landau & Lifshitz Classical Mechanics where it is stated that

enter image description here

Now I get that $\delta S= \delta S' =0$, for this to be true $\delta f(q^{(2)}, t_2) =\delta f(q^{(1)}, t_1)$. $$ \frac{\partial f(q,t_2)}{\partial q} dq = \frac{\partial f(q,t_1)}{\partial q}dq $$
Now my claim is that $dq$ is zero at the endpoints since endpoints are fixed (because $t1$ and $t2$ are fixed) (we use this fact while deriving the Lagrangian equations as well). And hence the Lagrangian differing by the the time derivative of any function are equivalent. Is my reasoning correct? The start and end times being fixed doesn't necessarily imply start and end points are fixed. My mathematical proof is not rigorous enough. Does anyone else have a better explanation?

Karel
  • 2,520
Shankar R
  • 31

1 Answers1

1

Now I get that $\delta S= \delta S' =0$, for this to be true $\delta f(q2, t2) =\delta f(q1, t1)$.

Yes. But, there is a stronger statement, namely that: $$ \delta f(q_2, t_2) = \delta f(q_1, t_1) = 0\;. $$ I.e., they are equal because they are both equal to zero.

Is my reasoning correct?

Seems to be.

My mathematical proof is not rigorous enough.

This seems to be a matter of opinion.

Does anyone else have a better explanation?

Another way to put it is that equations of motion result from minimizing the action for all paths with fixed endpoints $(q_2, t_2)$ and $(q_1, t_1)$.

From the very beginning, if you are trying to generate the equations of motion, the only variations you are allowed to consider have the endpoints fixed. So, by definition of the paths you are allowed to consider, you automatically have $\delta f(q_2, t_2) = 0$ and $\delta f(q_1, t_1) = 0$.

hft
  • 27,235