I'm currently studying Landau's mechanics book and am wondering about the "Lagrangian for a free particle" part.
If an inertial frame K is moving with an infinitesimal velocity $\vec{\epsilon}$ relative to another inertial frame K‘, then $\vec{v}' = \vec{v} + \vec{\epsilon}$.
And then:
$\mathcal{L}' = \mathcal{L}(v'^2) = \mathcal{L}(v^2 + 2\vec{v} \cdot \vec{\epsilon} + \epsilon^2)$. Expanding this expression in powers of $\epsilon$ and neglecting terms above the first order, we obtain: $$ \mathcal{L}(v'^2) = \mathcal{L}(v^2) + \frac{\partial L}{\partial v^2} 2\vec{v} \cdot \vec{\epsilon} $$
Why must the relative velocity $\epsilon$ be very small?
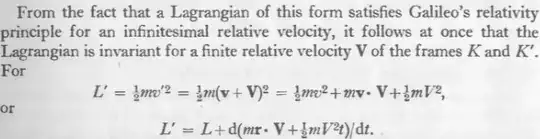
And I also don't understand this part, why from the very small relative velocity $\vec{\epsilon}$ we infer this to the finite relative velocity $\vec{V}$?
Please help me, thanks.