Is it spacetime curvature or space-"rate of time" curvature?

Question

Here is a simple 2D diagram of 4D spacetime, showing curvature caused by a massive object, as it's commonly depicted:

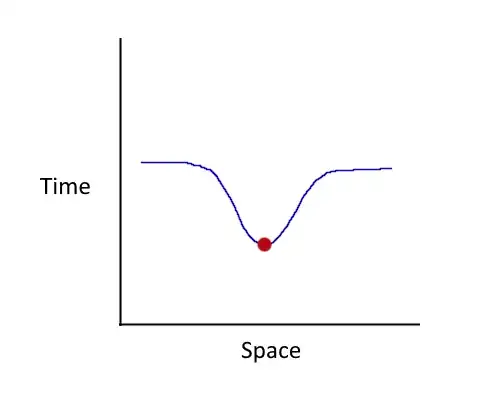
Here we see based on the diagram that the object is "back in time" compared to the surrounding area where the curvature is less dramatic. This statement on its own would seem correct, as we know massive objects slow time, causing the object to "fall behind" in its time compared to less massive objects. However, this whole depiction is not correct-- it can't be correct-- as if it were accurate it would mean one of two things: either the massive object would move "down" in the time dimension relative to the surroundings as the discrepancy between the clocks of the massive object and the surrounding area grew further and further out of sync, causing the spacetime curvature of the massive object to increase over time, or, time won't move at any different rate for the massive object, it will simply be offset or out-of-sync by a certain amount, given by the vertical offset in the graph.

Neither of these descriptions match observed reality, so the depiction must be wrong. The problem seems to be in depicting spacetime curvature as an offset in the time coordinate. We understand that it's not the point in time that's offset by spacetime curvature, but the rate of time.

Given that, here's a simple correction to the diagram:

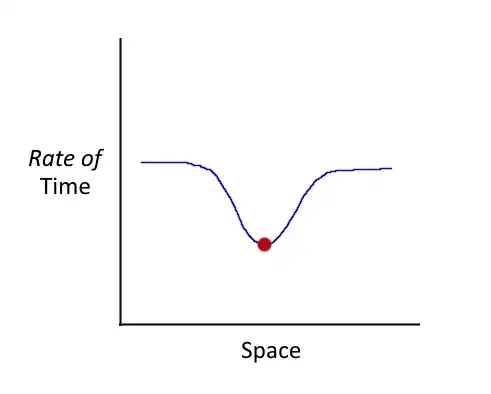
This change seems to align the common visual with observed reality, but there is another problem: "rate of time" isn't a physical dimension, right? The fourth dimension we talk about is always labelled time, not "rate of time," and a rate of something can't be a physical dimension, right?

I have until now always understood spacetime curvature as curvature "into" the time dimension, but is that simply untrue? Or at least in the simple sense? What is going on exactly with spacetime curvature then?

Answer 1

It is space-rate (of time). However, rate in this case has the units $$ (\text{interval}) \times \text{interval}^{-1} $$ ...meaning time periods distributed over time. This is analogous to lengths distributed over length (eg: tiles). Physically speaking, these units are used to quantify the speed of time in different regions of space as scalar multiples of each other, usually by setting the rate of the reference region to 1. It is significant in coordinate systems with time scale symmetry, where the passage of time is invariant under rescaling across all spatial locations.

Answer 2

"rate of time" isn't a physical dimension, right?

It's not entirely clear that time itself is a "physical" dimension.

A static, 3D description is clearly not sufficient to account for the physical world, because we can see motion through space, we can see change.

But motion through time itself - the "flow" of time, or the assumption that things present in space are constantly hurtling through time - is a conception for which the physical evidence is actually quite unclear.

Clocks certainly do not measure pure motion through time. They measure motion through space, often with some internal element that is spatially-oscillating, though alternatively they may employ some mechanism that meters a flow of matter or energy from one place to another. They measure the rate of this spatial motion.

It is often difficult to discern where the "forwardness" of the motion is in clocks with oscillators, whereas metering-style clocks like hourglasses often require resets that reverse them to their initial conditions (again putting into question the "forwardness" of the overall technique, as the sand keeps ending up back in the upper bulb of the glass).

In a pendulum clock for example, there is an auxiliary mechanism that forces the outward clock reading to proceed in one direction. The pendulum itself goes forth and back, and the escapement simply discards the effect of one direction or employs it in an asymmetric way.

Real pendulums are subject to frictional losses which mean it does not recover a previous state fully on each swing, but it is not clear that this fictional loss plays any part in what is actually measured by such a clock - in theory, a clock with a frictionless pendulum would appear to function as a clock (even better so, in fact), so the friction cannot bear the role of demonstrating that such a clock is measuring something proceeding forward.

In my view physics is in a mess regarding these issues.

The 2nd law of thermodynamics, which is often quoted in support of the idea that time flows, was formulated in the 19th century by those describing the empirical behaviour of heat engines. It was not intended to be a profound philosophical statement about the nature of time.

The seeming non-recurrence of the state of the universe is ultimately a non-local observation - that is, it is not how any man-made clock machine with an internal mechanism works - and whether the state of the universe does ultimately recur is a cosmological question, the alleged forwardness is certainly not science.

Ultimately, whether the flow of time is altered or the "time dimension" is curved, or whether the rate of clocks are altered, it is not clear. Indeed, because the alleged flow of time or placement within the time dimension is measured by the rate of clocks, it is not even clear if there is a physical distinction between "curving the time dimension" and "changing the rates of clocks", the only distinction being whether we are talking directly about physical things (the "rates of clocks") or whether we are talking about the physical world after it has been reduced to a particular mathematical analysis (the "time dimension").