Assuming you could go faster than light in Minkowski spacetime, how could you close your worldline?

Question

I've been looking into how faster-than-light travel implies time travel. I'm familiar with the simplest example to show that causality is violated with faster-than-light communication (the example I found is here: Why FTL implies time travel). So far as I can tell, this violates causality by sending information of an event that has not yet occurred, but does not present the ability for "time travel" in the sense of a closed worldline (meeting yourself in the past).

Using only special relativity, and the assumption that you can travel faster-than-light in Minkowski spacetime, can you create a closed worldline? If so, what would the Lorentz transform look like? Also, assuming you had an infinite amount of time, could you close your worldline at any speed faster than light?

Answer 1

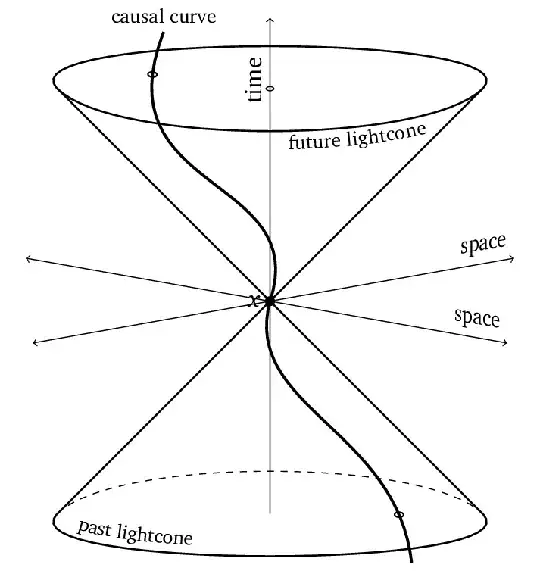
I've been looking into how faster-than-light travel implies time travel.

You're very much into the realm of science fiction with this.

The problem is:

I'm familiar with the simplest example to show that causality is violated with faster-than-light communication

...the very definition of "casuality" in this context already incorporates the assumption that nothing can travel FTL. If something were discovered that did travel FTL, then the existing predominant interpretation of casuality in physics must already collapse as a result.

Time travel would not be implied, because that implication only arises if you allow the current definition of causality to remain standing without one of its necessary assumptions.

Therefore you would have to make two interlinked assumptions to pose this question. You would have to ask, what happens if we have FTL and we don't use our current definition of causality?

Well, what other definition of causality are you proposing?

And would geometric models and concepts like "worldlines" still be valid/applicable under those circumstances? No, because they too depend on the existing speed limit and definition of causality to work, both of which you've overhauled in the process of setting up this hypothetical - one overhauled by direct choice, the other overhauled by necessary implication of that choice.

It's also worth noting, if you allow your model of physics to become completely disintegrated and are willing to innovate any part of it a la carte, then anything is possible really. Your worldline could be closed by a wizard - a specific worldline-closing wizard even. But that wouldn't be physics.

It's sometimes useful to pose hypotheticals to tease out the relationships and constraints between concepts, but in this case, what is revealed is the mutual dependency between the speed of light and the way causality is currently defined.

Answer 2

Take a helix curve loop with $0<t< 2\pi T$, \begin{eqnarray*} x(t)=R \cos(t/T),\\ y(t)=R \sin(t/T), \end{eqnarray*} For $R/T>c$ this will be always spacelike.

Then connect it to the reflected helix, \begin{eqnarray*} x(t)=R \cos(t/T),\\ y(t)=-R \sin(t/T), \end{eqnarray*} After doing such connection you get a closed spacelike curve with cusps at $t=0$ and $t=2\pi T$. You now may deform the curves near those points to obtain a smooth closed spacelike curve, containing a point $t=2\pi T$ that is in a future lightcone of another point $t=0$ of a curve.

This will correspond to a superluminal particle going to a future, then "accelerating" in such a way that it travels to the past and returning back to the original point in spacetime.

As for the "acceleration". There is no reference frame in which a superluminal particle will be at rest. There are however reference frames where its 4-velocity have a zero temporal component i.e. particle have infinite velocity. Boosting in one direction this 4-velocity gains a positive temporal component - particle travels to the future with a finite velocity $>c$. Boosting in a another direction this temporal component becomes a negative one - the particle travels to the past.

Answer 3

If you'll look at a spacetime diagram like the one below, you'll see that spacetime is divided into the regions inside the future and past light cones, and everything else which are events space-like separated from the origin.

The worldline of an object traveling faster than light, starting at the origin, will be represented on this diagram as a line outside the future lightcone, so for example it will connect the point $(0,0)$ to some $(x,t)$ where $x>t$ (using units where $c=1$).

Now, an important property of Lorentz symmetry is that all space-like directions are "the same" (in an equivalent manner to how all spatial directions are "the same" under rotational symmetry). This means that the fact the this line appears to be in the future direction on our chart is just a matter of coordinates system choice - we can choose a different coordinate system in which the same line will go to the past. Indeed we can apply a Lorentz transformation

$$t' = \gamma(t - vx)$$ $$x' = \gamma(x-vt)$$

in which $t'<0$, by choosing $v$ such that $t/x > v > 1$. We can do this because $x>t$.

Now you can easily continue drawing space-like curves like that until you reach a point in the past light cone, which means that you can close a loop and return to your starting point.

,

Answer 4

Let's take Minkowski spacetime interval along $x$ coordinate,

$$ \begin{align} s^2&=−c^2 \Delta t^2+\Delta x^2\\ &=−c^2 \Delta t^2 + v_x^2 \Delta t^2\\ &=\Delta t^2\left(-c^2+v_x^2\right) \end{align}$$

When $v_x \gt c$, then it implies that $s^2 \gt 0$ and so interval becomes spacelike, which means that your travel initial point and destination is not causally connected at all. So if you plan travel between cities $A\to B\to C$, you may as well go in reverse order $C\to B\to A$ even this travel is causally disconnected and at normal conditions would be forbidden. And that basically means that you inverted arrow of time.

Or think in this way,- if you plan to leave city $A$ and go to $B$ and then return back to $A$,- you might as well return to $A$ even without leaving it ! Again this type of thing can't be if your travel spacetime points are causally connected and so for it to happen some sort of time-travel is required.