Whenever:
are put in form of a function, they are either represented as sinusoidal or cosinusoidal functions.
What's the reason behind choosing these trigonometric functions to represent them? Why not represent them using some other oscillating function?
Because typical scalar wave equation has form, $$ \tag 1 \ddot u = v^2 \nabla ^2 u ,$$ to which plane-wave eigenmodes (with a constant frequency) temporal part has form $$ \tag 2 u(t) = C e^{-i\omega t} ,$$ where $C$ being some complex amplitude carrying wave phase information.
According to Euler's formula,
$$ \tag 3 e^{ix}=\cos x+i\sin x $$
real part of (2) can be rewritten as,
$$ \tag 4 Re[u(t)] = A \cos(\omega t) $$
Hence, the periodic function $\cos()$ in the scalar field temporal fluctuation. As an additional bonus, $\sin/\cos$ works very good in Fourier transform, i.e. signal can be split into different harmonics, where multiple sine/cosine waves interferes with each other producing final wave. Not to mention that for this analysis wave defining function $u(t)$ must be differentiable and continuous, which applies to periodic trigonometric functions, like sine.
Sure, general form of scalar wave solution does not have to be bound only by raw trigonometric functions, as it is in the form, $$ \tag 5 u(x,t)=F(x-vt)+G(x+vt). $$
And so you can also have Sawtooth wave signal, like
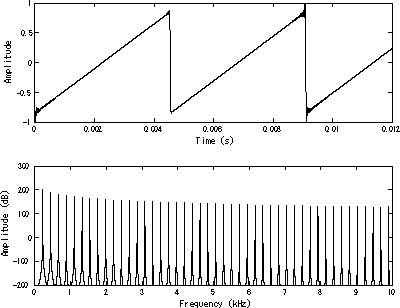
but since $F(),G()$ are not differentiable here, you need to fallback to numerical methods like Discrete Fourier transform for component analysis, which may or may not be cumbersome. So once again- periodic differentiable functions like $\sin,\cos$ makes analytical wave analysis approachable.
If you want to study any kind of continuous change (change of the position of a body over time, change in the rate of airflow over an airplane wing with respect to the airplane's attitude, change in the color of the sky with respect to altitude at sunset,... any kind of change at all) then you will either end up using or re-inventing calculus.
If you want to study any kind of continuous change that involves a periodic function (rotary motion, ocean waves, pendulums, organ pipes, instabilities in the HVAC system of a large office building,... any situation that continually repeats itself) then you will end up using sines and cosines.
Sines and cosines are the absolutely simplest periodic functions that can be studied with calculus. Calculus requires functions that are differentiable, and sines and cosines are infinitely differentiable. Not only that but, if you differentiate $sin(x)$ or $cos(x)dx$ four times with respect to $x$, you come back to exactly where you started—differentiating them does not complicate them.
Finally, it's been proven that any periodic function can be decomposed as a series of sines and cosines, which kind of puts a cap on the whole thing. If you want to study continuous, periodic change, then there's really no reason to model it in any other way.
Sine or cosine functions are harmonic waves and solutions of Maxwell equation. From mathematical point of view, they have important properties like orthogonality and they are describing all the solutions of the equations. So if you have a harmonic solution, in principle you can construct other solutions when, for example the excitation is another periodic signal. Another problem is when one has an impulses, they are possible for Maxwell equation, then the basis functions are $e^{st}$ where $s$ is complex. Also, you can imagine other basis functions, like harmonic signal limited by a gaussian envelop. Anyway, the basis function - a wavelet depends on the application. Usually it is simple to use harmonic $\sin$ and $\cos$ for common applications. Like for an emission of an antenna where we know that a boundary condition is a harmonic current that will emit a harmonic wave
in simplified cases when wave is made by something in simple harmonic motion, ie, acceleration is propotional to distance from mean position, we get a sine wave
and in other complicated cases we use fourier analysis. This idea basically says that any repeating pattern, no matter how complicated it looks, can be broken down into a combination of simple sine waves and cosine waves. So, even if a wave isn't a perfect sine wave, we can still describe it by adding together a bunch of sine waves with different frequencies and sizes. It's like having a set of building blocks (the sine waves) that you can use to construct any kind of wave shape.
While there are other mathematical functions that oscillate, sine and cosine waves are particularly useful because they're smooth, their derivatives are also nice and smooth, and they just naturally appear in the equations that govern many physical phenomena. They provide a really elegant and powerful way to understand and analyze waves, which is why they're so fundamental in physics and engineering.
The wave equation, which is used to model all of the types of waves that you mention, is a linear differential equation, and its solutions are sine/cosine waves and linear superpositions of such waves. So it is natural to think of any wave as a combination of sinusoidal components with different amplitudes, and there is a whole branch of mathematics called Fourier analysis that is devoted to approximating arbitrary periodic functions in this way.
However, if we are dealing with a nonlinear medium then the wave equation becomes more complicated, it no longer has simple sinusoidal solutions, and the superposition principle no longer holds - so modelling waves in a non-linear medium is much more complicated (although a first step may still be to start with a linear approximation).
The reason behind the choice of sinusoidal or cosinusoidal functions, stems from the periodic nature of these functions..
All periodic functions can be represented by a closed curve mathematically. The simplest closed curve one can think of its a circle....
So every periodic motion, or oscillatory motion can be represented by a circle of some radius....and making use of pythegorus theorem, you get a relation of trigonometric functions to explain the motion.
Fourier realised that any function can be made periodic if it is a linear combination of trigonometric functions....since these are the only periodic functions...
So the reason behind the representation of oscillatory motion using trigonometric functions, stems from the nature of these functions.
All other functions can be related to them, like for instance Euler's equation.
I want to expand slightly on the answer of Agnius Vasiliauskas. The differential equation $\ddot u=v^2\nabla^2 u$ reduces to $\ddot u=v^2u''$ in 1d, as in the example of waves travelling on a string. I'm going to treat this case for simplicity.
A standard method to solve such partial differential equations is to assume that the solution $u(x,t)$ can be decomposed into a product of a spacial part $f(x)$ and a temporal part $g(t)$ like $u(x,t)=f(x)g(t)$. Substituting into the PDE gives
$$f(x)\ddot g(t)=v^2f''(x)g(t),$$
which can be rearranged to
$$\frac{\ddot g(t)}{g(t)}=v^2\frac{f''(x)}{f(x)}.$$
Note that the left side depends on $t$ only, while the right side depends on $x$ only. So because the left side doesn't depend on $x$, the right side doesn't either, and the same argument applies to the left side and its dependence on $t$. Both sides must be constant. The constant can be any number $k$, unless physics dictates something specific, for instance through boundary conditions. So we have a pair of ODEs
$$\frac{\ddot g(t)}{g(t)}=k,~~~v^2\frac{f''(x)}{f(x)}=k$$
for all $k$, and the product of the solutions is a solution to the PDE. And you guessed it, the solutions to these ODEs are trigonometric functions. All other solutions are sums (or possibly integrals) of these simpler trigonometric solutions.
Ask a kid to draw a wave and the result will be a sine. That’s why.
Edit after downvote:
99% of kids draw a sine.
