Which sequence of rotations is correct here?

Question

I have a problem of understanding the sequence of rotations in 3d space.

Assuming I have an object (airplane/vehicle/etc.) with a device that measures angular velocities of yaw, pitch, roll $\dot{\alpha}(t),\dot{\beta}(t),\dot{\gamma}(t)$. Assume also that position ($x(t),y(t),z(t)$) of center of gravity (cog) is known/measured and all rotations are around cog.

By numeric intergration I can compute $\alpha(t),\beta(t),\gamma(t)$ from the derivatives (assume accuracy of integration is not an issue).

Then at some specific time $t_s$ I have a specific position $(x_s,y_s,z_s)=(x(t_s),y(t_s),z(t_s))$ and a specific orientation $(\alpha_s,\beta_s,\gamma_s)=(\alpha(t_s),\beta(t_s),\gamma(t_s))$.

Assuming my object is represented by a list of $n$ points $(x_i,y_i,z_i)$ with $i=1,\dots,n$. Then I can set the orientation of my object by $$ X_i'=R(X_i-X)+X $$ where $$ X_i=\begin{pmatrix} x_i\\y_i\\z_i \end{pmatrix},X=\begin{pmatrix} x\\y\\z \end{pmatrix} $$ and a rotation matrix $R$. Lets assume for simplicity that $X=0$, i.e. the object didn't move its cog but just did a rotation.

Since the order of rotations matter, how can I know which $R$ is the "physically correct" one, which will give me the correct orientation that my object has in reality, based on the measurements?

Is it $$ R_1=R_z(\alpha_s)R_y(\beta_s)R_x(\gamma_s) $$ or $$ R_2=R_x(\gamma_s)R_y(\beta_s)R_z(\alpha_s) $$ or something different? How can I know the correct order? Here: $$ R_z(\alpha)=\begin{pmatrix} \cos(\alpha)&-\sin(\alpha)&0\\ \sin(\alpha)&\cos(\alpha)&0\\ 0&0&1 \end{pmatrix} $$ $$ R_y(\beta)=\begin{pmatrix} \cos(\beta)&0&\sin(\beta)\\ 0&1&0\\ -\sin(\beta)&0&\cos(\beta) \end{pmatrix} $$ $$ R_x(\gamma)=\begin{pmatrix} 1&0&0\\ 0&\cos(\gamma)&-\sin(\gamma)\\ 0&\sin(\gamma)&\cos(\gamma) \end{pmatrix} $$

Example: Assume the object in question is a cube with $$ X_i=\begin{pmatrix} \pm 1\\\pm 1\\\pm 1 \end{pmatrix} $$ so $n=8$ for all sign permuations and cog at the origin. Take $\alpha_s=10°,\beta_s=20°,\gamma_s=30°$. Then I get the following result:

Black = original ($\alpha_s=0,\beta_s=0,\gamma_s=0$.), blue = using $R_1$, red = using $R_2$. Clearly, blue and red do not overlap. However only one configuration can be correct given the measurements.

Answer 1

Having the three Euler angles is not sufficient to determine the rotation matrix, because you also need to know the sequence of rotations and the convention used about which axis the rotations happen.

It is not like the three Euler angles appear out of nowhere. You need to decide those things in advance to get to them and be consistent with them. The choice usually revolves around how to avoid gimbal lock.

There are some conventions common to aviation, or robotics for example, but they are not laws, and are up to the user to implement them correctly.

To eliminate these issues often people uses the quaternion representation to encode rotations which does not need predetermined fixed axes of rotation.

To convert a rotation matrix $\mathrm{R}$ to a quaternion $\boldsymbol{q} = (s,\,\vec{v})$ you do the following

$$\begin{aligned}s & =\frac{1}{2}\sqrt{\frac{\left(\mathrm{R}_{32}-\mathrm{R}_{23}\right)^{2}+\left(\mathrm{R}_{13}-\mathrm{R}_{31}\right)^{2}+\left(\mathrm{R}_{21}-\mathrm{R}_{12}\right)^{2}}{3-\mathrm{R}_{11}-\mathrm{R}_{22}-\mathrm{R}_{33}}}\\ \vec{v} & =\frac{1}{4s}\begin{pmatrix}\mathrm{R}_{32}-\mathrm{R}_{23}\\ \mathrm{R}_{13}-\mathrm{R}_{31}\\ \mathrm{R}_{21}-\mathrm{R}_{12} \end{pmatrix} \end{aligned}$$

and now to do a time integration of the quaternion with $\boldsymbol{q} \leftarrow \boldsymbol{q} + \dot{\boldsymbol{q}} \Delta t$ where the quaternion rate depends on angular velocity $\vec{\omega}$ with $$\begin{aligned}\dot{\boldsymbol{q}} & =\frac{1}{2}\boldsymbol{\omega}\,\boldsymbol{q}\\ \begin{pmatrix}\dot{s}\\ \dot{\vec{v}} \end{pmatrix} & =\frac{1}{2}\begin{pmatrix}0\\ \vec{\omega} \end{pmatrix}\begin{pmatrix}s\\ \vec{v} \end{pmatrix}=\frac{1}{2}\begin{vmatrix}0 & -\vec{\omega}^{\intercal}\\ \vec{\omega} & \vec{\omega}\times \end{vmatrix}\begin{pmatrix}s\\ \vec{v} \end{pmatrix}=\frac{1}{2}\begin{pmatrix}-\vec{\omega} \cdot \vec{v}\\ s\,\vec{\omega}+\vec{\omega}\times\vec{v} \end{pmatrix} \end{aligned}$$

and finally building the rotation matrix from the next quaternion $\boldsymbol{q}=(s,\vec{v})$ with

$$\begin{aligned}\mathrm{R} & ={\bf 1}+2s[\vec{v}\times]+2[\vec{v}\times][\vec{v}\times]\\{} [\vec{v}\times] & =\begin{pmatrix}0 & \text{-}v_{z} & v_{y}\\ v_{z} & 0 & \text{-}v_{x}\\ \text{-}v_{y} & v_{x} & 0 \end{pmatrix} \end{aligned}$$

Answer 2

$\def \b {\mathbf}$ To obtain the transformation matrix between the Body system and Inertial system $~\b R(t)~$ you can use those two methods

Method I

with the transformation matrix \begin{align*} &\b R=\b R_z(\psi)\,\b R_y(\theta)\,\b R_x(\phi) \end{align*} where $~\psi~$ is the yaw angle, $~\theta~$ is pitch angle and $~\phi~$ is the roll angle.

from the transformation matrix you obtain \begin{align*} &\begin{bmatrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \end{bmatrix}= \left[ \begin {array}{ccc} 1&{\frac {\sin \left( \theta \right) \sin \left( \phi \right) }{\cos \left( \theta \right) }}&{\frac {\sin \left( \theta \right) \cos \left( \phi \right) }{\cos \left( \theta \right) }}\\ 0&\cos \left( \phi \right) &-\sin \left( \phi \right) \\ 0&{\frac {\sin \left( \phi \right) }{\cos \left( \theta \right) }}&{\frac {\cos \left( \phi \right) }{\cos \left( \theta \right) }}\end {array} \right] \,\begin{bmatrix} \omega_1(t) \\ \omega_2(t) \\ \omega_3(t) \\ \end{bmatrix}\tag 1 \end{align*} for a given $~\omega_i(t)~$ the solution of those 3 differential equations with the initial conditions $~\psi(0)=0~,\theta(0)=0~,\phi(0)=0~$ is $~\psi(t)~,\theta(t)~,\phi(t)~$

Method II

\begin{align*} &\b{\dot{R}}=\b R\, \left[ \begin {array}{ccc} 0&-\omega_{{3}} \left( t \right) &\omega_{ {2}} \left( t \right) \\ \omega_{{3}} \left( t \right) &0&-\omega_{{1}} \left( t \right) \\ - \omega_{{2}} \left( t \right) &\omega_{{1}} \left( t \right) &0 \end {array} \right] \tag 2 \end{align*} the solution of the 9 differential equations with the initial conditions

$~R_{11}(0)=1 ,~R_{22}(0)=1 ,~R_{33}(0)=1\quad, R_{ij}(0)=0~, i\ne j$

is the transformation matrix $~\b R(t)~$, where the input is the angular velocities $~\omega_i(t)~$

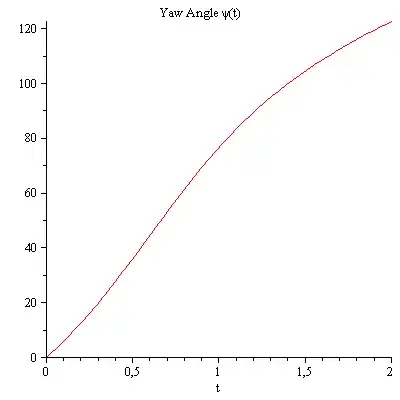
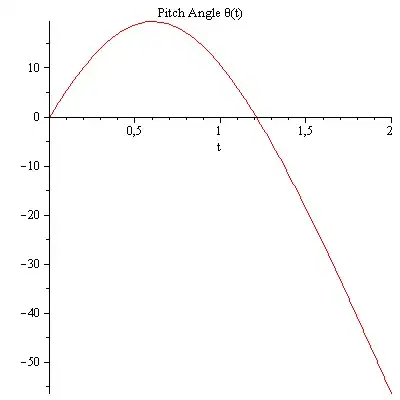
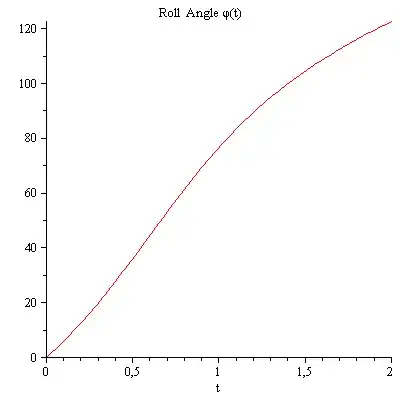
yaw ,pitch ,roll angles

\begin{align*} &\psi(t)=\arctan\left(R(t)_{21},R(t)_{11}\right)\\ &\theta(t)=\arctan\left(-R(t)_{31},\sqrt{R(t)^2_{11}+R(t)^2_{21}}\right)\\ &\phi(t)=\arctan(R(t)_{32},R(t)_{33}) \end{align*}

Simulation

\begin{align*} \b\omega(t)=\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \end{align*} compare the yaw, pitch and roll angles both methods

---

• More details on Method I and II

Remarks

• the body fixed coordinate system is located at the center of mass where the x- axis is to the front, the y-axis to the left and the z-axis $~\b z=\b x\times \b y~$

• the components of angular velocity vector $~\b\omega~$ are given in body system

• with equation (1), you get singularity if the pitch angle $~\theta=\pi/2~$

• it is easy to use equation (1) then equation (2)

• How to obtain for a arbitrary rotation matrix the yaw pitch and roll angles

compare arbitrary rotation matrix R with the rotation matrix of method I.

\begin{align*} & \left[ \begin {array}{ccc} R_{{1,1}}&R_{{1,2}}&R_{{1,3}} \\ R_{{2,1}}&R_{{2,2}}&R_{{2,3}} \\ R_{{3,1}}&R_{{3,2}}&R_{{3,3}}\end {array} \right] =\b R_z(\psi)\,\b R_y(\theta)\,\b R_x(\phi)=\\&\left[ \begin {array}{ccc} \cos \left( \psi \right) \cos \left( \theta \right) &-\sin \left( \psi \right) \cos \left( \phi \right) + \cos \left( \psi \right) \sin \left( \theta \right) \sin \left( \phi \right) &\sin \left( \psi \right) \sin \left( \phi \right) +\cos \left( \psi \right) \sin \left( \theta \right) \cos \left( \phi \right) \\ \sin \left( \psi \right) \cos \left( \theta \right) &\cos \left( \psi \right) \cos \left( \phi \right) + \sin \left( \psi \right) \sin \left( \theta \right) \sin \left( \phi \right) &-\cos \left( \psi \right) \sin \left( \phi \right) +\sin \left( \psi \right) \sin \left( \theta \right) \cos \left( \phi \right) \\ -\sin \left( \theta \right) &\cos \left( \theta \right) \sin \left( \phi \right) &\cos \left( \theta \right) \cos \left( \phi \right) \end {array} \right]\\ &\Rightarrow\\ &\tan(\psi)=\frac{R_{21}}{R_{11}}\quad, \tan(\theta)=\frac{-R_{31}}{\sqrt{R^2_{11}+R^2_{21}}}\quad, \tan(\phi)=\frac{R_{32}}{R_{33}} \end{align*}

to avoid singularity one can use instead of the Euler angles quaternion $~\b q\,(4\times 1)~$

The relationship between quaternions and angular Velocity vector

\begin{align*} \underbrace{\begin{bmatrix} \dot{q}_w \\ \dot{q}_x \\ \dot{q}_y \\ \dot{q}_z \\ \end{bmatrix}}_{\b{\dot{q}}}=\frac{1}{2} \left[ \begin {array}{cccc} 0&-\omega_{{x}}&-\omega_{{y}}&-\omega_{{z }}\\ \omega_{{x}}&0&\omega_{{z}}&-\omega_{{y}} \\ \omega_{{y}}&-\omega_{{z}}&0&\omega_{{x}} \\ \omega_{{z}}&\omega_{{y}}&-\omega_{{x}}&0 \end {array} \right]\,\underbrace{\begin{bmatrix} {q}_w \\ {q}_x \\ {q}_y \\ {q}_z \\ \end{bmatrix}}_{\b q(t)} \end{align*} where the components of $~\b\omega~$ is given in body system

solving the differential equations with the initial conditions

$q_1(0)=1~,q_i(0)=0~,i=2..4~$ you obtain the solution $~\b q(t) ~$ where $~\b q(t)\,\cdot\,\b q(t)=1~$

The rotation matrix between the body and inertial system ,corresponding to a quaternion $\b {q}$

\begin{align*} \b R=\left[ \begin {array}{ccc} {q_{{1}}}^{2}+{q_{{2}}}^{2}-{q_{{3}}}^{2}- {q_{{4}}}^{2}&-2\,q_{{1}}q_{{4}}+2\,q_{{2}}q_{{3}}&2\,q_{{1}}q_{{3}}+2 \,q_{{2}}q_{{4}}\\ 2\,q_{{1}}q_{{4}}+2\,q_{{2}}q_{{3 }}&{q_{{1}}}^{2}+{q_{{3}}}^{2}-{q_{{4}}}^{2}-{q_{{2}}}^{2}&-2\,q_{{1}} q_{{2}}+2\,q_{{3}}q_{{4}}\\ -2\,q_{{1}}q_{{3}}+2\,q_ {{2}}q_{{4}}&2\,q_{{1}}q_{{2}}+2\,q_{{3}}q_{{4}}&{q_{{1}}}^{2}+{q_{{4} }}^{2}-{q_{{2}}}^{2}-{q_{{3}}}^{2}\end {array} \right] \end{align*}