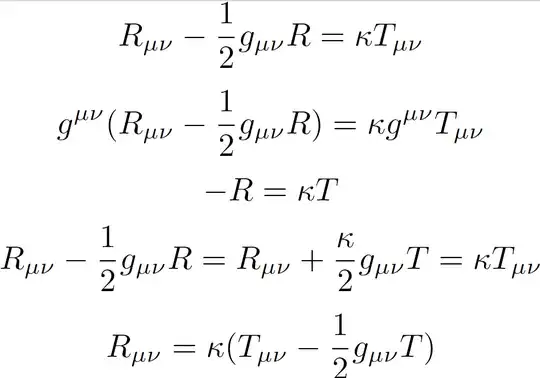I do not understand derivation of the 3rd line below. This follows from $$-\frac{1}{2}g_{\mu\nu}g^{\mu\nu}R=-2R$$ and even if it does not, I do not follow the 3rd line$-$how it follows. More precisely: why in general $g_{\mu\nu}g^{\mu\nu}=4$. For diag(-1,1,1,1) this holds.
2 Answers
$$g^{\mu\nu}(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R) =\kappa g^{\mu\nu}T_{\mu\nu}$$
$$\underbrace{g^{\mu\nu}R_{\mu\nu}}_{=R} -\frac{1}{2}\underbrace{g^{\mu\nu}g_{\mu\nu}}_{=\delta^\mu_\mu=4}R =\kappa \underbrace{g^{\mu\nu}T_{\mu\nu}}_{=T}$$
$$R-\frac{1}{2}4R=\kappa T$$ $$-R=\kappa T$$
- 42,352
I am not too sure what type of answer you want. I will try to answer with the limited knowledge I have about tensors. In differential geometry/GR, we want objects to be invariant, so we use tensors. On a manifold $M$, a vector is an element of the tangent space $V\in T_p$ at a point $p$. The vector is a (1,0)-tensor written as $$ V = V^\mu\partial_\mu, $$ where $\partial_\mu$ is the basis vector, and $V^\mu$ the components. We also have the dual tangent space $T_p^*$ of linear forms $\omega:T_p\to\mathbb{R}$ on $T_p$ with $$ \omega=\omega_\mu dx^\mu, $$ where the basis vectors are $dx^\mu$. We can always choose the dual basis such that $$ dx^\mu(\partial_\nu) = \delta^\mu_\nu. $$ The metric tensor is defined a linear map from two copies of the tangent space $T_p$ into the reals, $g:T_p\times T_p\to \mathbb{R}$, given as $$ g \equiv g_{\mu\nu}dx^\mu\otimes dx^\nu, \quad g(V,W)= g_{\mu\nu}V^\mu W^\nu\equiv V\cdot W. $$ If we don't specify one of the arguments in the metric-tensor, we can view it as a map from the tangent space to the cotangent space: $$ g(\cdot, V) = g_{\mu\nu}dx^\mu dx^\nu(V^\alpha\partial_\alpha) = g_{\mu\nu}V^\alpha dx^\mu\delta^\nu_\alpha = g_{\mu\nu}V^\nu dx^\mu = \tilde{V}_\mu dx^\mu\in T_p^*. $$ It is natural to then consider the inverse metric $g^{-1}$ such that when composed with $g$, it yields the identity tensor. Since the metric is a map from the tangent space to the cotangent space $T_p\to T^*_p$, the inverse metric is a map from the cotangent space to the tangent space, $T_p^*\to T_p$, written as $$ g^{-1}=g^{\mu\nu}\partial_\mu\otimes\partial_\nu. $$ Then $$ g^{-1}(\cdot, g(\cdot, V)) = g^{\mu\nu}\partial_\mu\otimes\partial_\nu(g_{\alpha\beta}V^\beta dx^\alpha) = g_{\mu\nu}g_{\alpha\beta}V^\beta\partial_\mu\delta^\alpha_\nu = V^\beta g^{\mu\nu}g_{\nu\beta}\partial_\mu $$ as this is the identity tensor, this must give back $g^{-1}(\cdot, g(\cdot, V))=V^\mu\partial_\mu$, hence $g^{\mu\nu}g_{\alpha\beta} = \delta^\mu_\beta$ is the only alternative. Consequently, the contraction $g^{\mu\nu}g_{\mu\nu}=\delta^{\mu}_\mu=d$ where $d$ is the spacetime-dimension.
- 336