Landau and Lifshitz's argument on the preservation of causality for time-like events

Question

Consider two events that are time-like in one inertial reference frame, now the corresponding interval will be positive in all frames i.e., $$ds^2=c^2(dt^2)-dl^2>0$$ but how does this guarantee that $dt>0$ in all the frames? I was reading Landau and Lifshitz vol.2 page 7. They say from the positive value of $ds^2$ for time-like events it follows that $dt\neq0$ in any frame, which makes sense. He then says that this preserves causality for time-like events i.e. $dt>0$, this is what has confused me, since from the above argument we could only infer that $c^2dt^2>dl^2$, but this doesen't guarantee that $dt>0$,since $dt$ could take negative values without violating the inequality.

Answer 1

Here is one way to do it based on continuity arguments alone. Assume for a moment Lorentz transformations are linear(look at this cool answer by user a06e https://physics.stackexchange.com/a/12858/304878) then two events as seen in the two different inertial frames S and S' are related by $\Delta x'_i =L^j_{i}(v)\Delta x_j $; i=0,1,2,3(Say S' moves with a velocity of v with respect to S). Here $\Delta x $ represents difference in coordinates of the two events in each of the frames S and S'.i.e.$\Delta x_i=(t_2-t_1,x_2-x_1,..)$ and $\Delta x'_i=(t'_2-t'_1,x'_2-x'_1,..)$.The crucial claim is that as I change my frames the $\Delta x_i$ 's would change continuosly when acted by the boost,i.e. each of $\Delta x'_i(\Delta x_j,v)$ is a continuos function with respect to the velocity v and $\Delta x'_i(\Delta x_i,v=0)=\Delta x_i$. For example a Lorentz boost L corresponding to an increment of the velocity by dv should result in a transformation of the difference of the coordinates by an infinitesimal amount etc.Now for a timelike interval $\Delta t\neq 0$ .If $\Delta t'$(v)(ignore the co-ordinate dependance for the moment) were positive in one frame there is no way it would be negative in another,otherwise Intermediate value theorem would guarantee that there is some v for which $\Delta t'$(v)=0.Hence causality is preserved for time-like intervals.

(Special thanks to Acuriousmind and NaturallyInconsistent for their patient discussions on chat.)

Answer 2

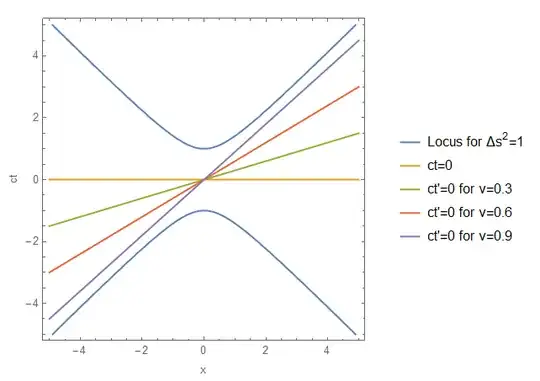
I think that this is easiest to see graphically. Here is a plot of the locus of all events with $\Delta s^2=1$. For convenience I am suppressing $y$ and $z$, but the conclusions hold if you include them (it just requires multiple plots to make the point instead of one).

On this plot I have also included the lines of events corresponding to $t=0$ and to $t'=0$ for frames moving at $v=0.3c$, $v=0.6c$, and $v=0.9c$ relative to the unprimed frame.

Note that the blue locus for $\Delta s^2=1$ includes events both above and below the yellow line for $ct=0$. Events above the yellow line are to the future of the origin for the unprimed frame, and events below the yellow line are to the past of the origin for the unprimed frame. The blue locus can thus be divided into two halves, a future half and a past half.

Now, consider the red line corresponding to $ct'=0$ for a frame moving with $v=0.6c$ relative to the unprimed frame. Events above the red line are to the future of the origin for the primed frame, and events below the red line are to the past of the origin for the primed frame. The blue locus can again be divided into two halves, a future half and a past half.

The key point is that as long as $-c<v<c$, all of the primed frames agree that all of the events on the top locus are to the future of the origin and all of the events on the bottom locus are to the past of the origin. In other words, they agree which half locus is the future and which is the past.

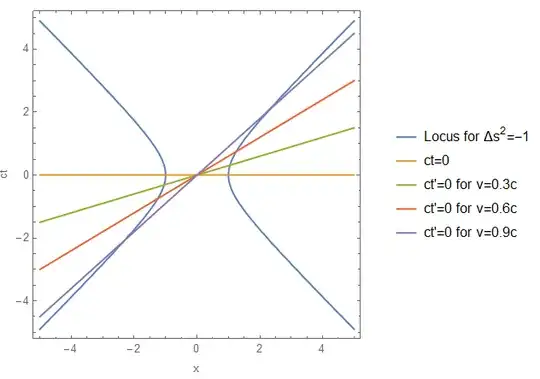
Note that the same thing is not true if we use $\Delta s^2=-1$

In that case the different frames do not agree which events on the locus are future and which are past. So you need to include both the (orthochronous) Lorentz transform and also the positive spacetime interval squared to conclude that the frames agree on the temporal ordering.