Differential equation for a heavy rope getting pulled upwards

Question

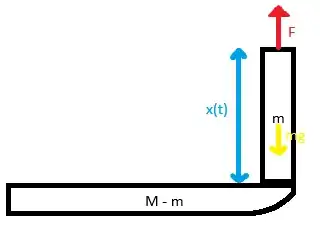
Suppose there's a non-stretchable rope sitting on a flat surface with total mass $M$ and length $L$. You pull one end upward with a constant force $F$. The part above the surface has mass $m$ and length $l$. Ignore thickness and friction. What is the differential equation that describes $l(t)$?

Original question: "A uniform 10-foot-long heavy rope is coiled loosely on the ground. As shown in FIGURE 1.R.2 one end of the rope is pulled vertically upward by means of a constant force of $5$ lb. The rope weighs $1$ lb/ft. Use Newton's second law in the form given in (17) in Exercises 1.3 to determine a differential equation for the height $x(t)$ of the end above ground level at time $t$. Assume that the positive direction is upward"

Attempt

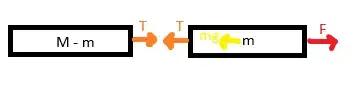
Newton's Second Law states that $F_{net}=\frac{d}{dt}[mv]$. The net force acting on the upper part (part above the surface) is $F_{net}=F - mg$ where we take the positive direction to be upward. The RHS becomes $\frac{dm}{dt} v + m\frac{dv}{dt}$. Assuming the rope has a constant density, $m=\frac{M}{L}l$.

$F - mg = \frac{dm}{dt} v + m\frac{dv}{dt}$

$F - mg = (\frac{M}{L}\frac{dl}{dt}) (\frac{1}{2}\frac{dl}{dt}) + (\frac{M}{L}l)(\frac{1}{2}\frac{d^2l}{dt^2})$

$\frac{M}{2L}(\frac{dl}{dt})^2+\frac{Ml}{2L}\frac{d^2l}{dt^2}+mg-F=0$

The reason why there's a $\frac{1}{2}$ is because the motion is of the center of mass; since $x_{CM} = \frac{l}{2}$, $v_{CM} = \frac{1}{2}\frac{dl}{dt}$ and $a_{CM} = \frac{1}{2}\frac{d^2l}{dt^2}$. The textbook seems to agree with my final equation but not about the $\frac{1}{2}$. I tried searching things up but it just seems to skip the fact that the center of mass and therefore its motion is half the length $l$. Am I wrong about something? Is it special that it is a rope? Is the textbook wrong?

Text: Advanced Engineering Mathematics 6th ed., Dennis G. Zill, Chapter 1 "Chapter in Review" problem 43

Answer 1

Okay. Regarding the comments and further research, including this Ján Lalinský argument (please read it), it turns out that both the textbook and I are wrong.

Newton's second law is not meant only for point masses, but for any massive body which does not lose or gain massive parts.

The model should also be considered from the top part (or any part that is clearly defined as a "part" and not something like, say the center of mass), as he writes:

It is also interesting to note that v in this equation is not velocity of the center of mass of the rocket, but velocity of its solid shell. It satisfies the relation p=mv where p and m are momentum and mass inside the (latter, close to the rocket surface) control volume. But because most of the mass gets lost, and center of mass moves closer to the tip of the rocket, this center moves somewhat faster than the solid rocket shell.

Figure 1 (left) and 2 (right) shows the situation and the forces, where the latter shows the tension force as the rope parts are displayed horizontally.

We can derive an equation similar to Ján Lalinský's equation (4): $$F_{ext} = \frac{dp}{dt} - \frac{dp_{out\rightarrow in}}{dt} \tag{1}$$ Where $F_{ext}$ includes all of the force exerted by the outside of the upper rope, including the parts that will enter the system. The $\frac{dp_{out\rightarrow in}}{dt}$ is the momentum of the infinismall part that will enter the system per $dt$. (The system here is the upper rope) Substitute $$F_{ext} = F - mg - T$$ $$\frac{dp}{dt} = m\frac{dv}{dt} + v\frac{dm}{dt}$$ $$\frac{dp_{out\rightarrow in}}{dt} = \frac{dm}{dt}v$$ into (1), we get $$F - mg - T = m\frac{dv}{dt} = ma \tag{2}$$ What's $T$? We know that the acceleration (and velocity) of the upper and the lower part must stay the same in order to stay together and not "rip". Since the lower part is also changing in mass, we derive a similar equation (derived from Ján Lalinský's (4)) $$T = (M-m)\frac{dv}{dt} - v\frac{dm}{dt} + v\frac{dm}{dt} = M \frac{dv}{dt} - m\frac{dv}{dt} = (M-m)a \tag{3}$$ Combine (2) and (3), $$a = \frac{F}{M} - \frac{m}{M} g$$ $$\frac{d^2h}{dt^2} = \frac{F}{M} - \frac{h}{L} g$$