Note that the term "free-fall" is used differently by laymen (from a physics "lens", it's misuse). For example: sky divers use free-fall to mean any part of the dive with nothing out, which ofc includes the terminal velocity phase.
We would call that "an object in motion tends to stay in motion if acted upon by no external force [lemma: or 2 or more forces that add to zero]".
So air resistance balances gravity and you fall at constant velocity (roughly, ofc the air is getting denser so you are slowing down--but we need some level of abstraction).
Regarding the edit that just appeared in the OP: "Is this a silly question?".
No, no it is not, and my qualitative answer is probably controversial, and a quantitative answer should require the major tools of General Relativity (GR).
Let's start out with just Newton: Free-fall is when the only external force acting on you ($m$) is:
$$ \vec F = -G\frac{Mm}{r^2} \hat r $$
You can determine this is the case experimentally by using an accelerometer:

If all 3-axises measure ZERO, you are in basic Newtonian free-fall.
A skydiver before air takes effect, ISS astronauts (esp. on EVA), the Vomit Comet:
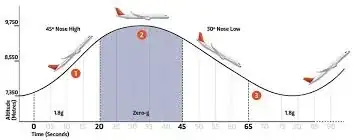
 or the classic: theoretical physicists in a broken elevator,
or the classic: theoretical physicists in a broken elevator,
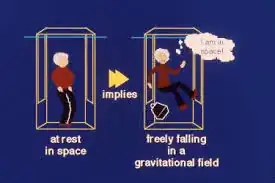
those are all standard "free-fall" scenarios. I was going to say. "If your trajectory is the ballistic trajectory, you are in free-fall", but the internet says "ballistic" includes drag and Magnus effect and all that--so you need to be careful!
Fortunately, the tools of physics (math) provide us with an unambiguous method to determine "free-fall". That tool is the Geodesic Equation (https://en.wikipedia.org/wiki/Geodesics_in_general_relativity):
$$ \frac{d^2x^{\mu}}{ds^2}
+\Gamma^{\mu}_{\alpha\beta}
\frac{dx^{\alpha}}{ds}
\frac{dx^{\beta}}{ds}
=0
$$
If your motion (along a path $x^{\mu}(s)$) in space-time is a solution of that equation, you are in free-fall.
It's a fantastic equation. It says you acceleration (plus some 4-velocity product with curvature) is zero.
In "space" (out there in flat Minkowski space time, with no gravity), it just says there is no acceleration, which is Newton's law.
Near a massive ($M$) spherical body, only the radial coordinate is non trivial, and the equation reads:
$$ \frac{d^2r}{dt^2} = -G\frac{M}{r^2} $$
That is, free-fall means accelerating downward at (Here, on Earth, at the surface):
$$ g = -G\frac{M_{\oplus}}{R_{\oplus}^2} = -9.82\,{\rm m/s^2} $$
It's a nice result, and the details are elsewhere on this site [todo: link].
In short: I think it is safe to say, that in free-fall, you have zero acceleration [in the right coordinates]. (However, gravity is non-linear, and I am reticent to make broad sweeping statements when:
$$ R \gg \frac{2GM}{c^2} $$
is violated.
Regarding my comment "in the right coordinates". Coordinates are a big deal. Even for the sky-diver falling ($\vec v$), the Earth ($M_{\oplus}$) is spinning ($\Omega_{\oplus}$)), and you will find that Newton:
$$ \vec F =-G\frac{Mm}{r^2}\hat r $$
doesn't quite work out. There is a centrifugal term:
$$ \vec F_c = -m\Big(\Omega_{\oplus}
\times (\Omega_{\oplus} \times r)\Big)
$$
and possiblly a non-zero Coriolis term:
$$ \vec F_C = -2m\Omega_{\oplus}\times \vec v$$
Note that these are so-called inertial forces (proportional to $m$). Some people call them "fictitious forces" because they depend on the choice of coordinates.
I consider them part of "gravitation", and are a required component of defining "free-fall".
The mathematical physicist can tell you General Relativity can be explained as follows: "Physical laws are covariant under coordinate diffeomorphisms", which in English means: "Physics doesn't care about your coordinate system". (This is a major rabbit-hole, and I am going to exit it now).
For us, it means that if you move along a geodesic, you are in free-fall and your accelerometers will all measure ZERO. Other observers may see you accelerating, but when they work out the effects "gravitation" (i.e., Newton's gravity plus fictitious forces, and they include gravio-electromagnetism (https://en.wikipedia.org/wiki/Gravitoelectromagnetism)), those are the only external forces acting on you, and that is "free-fall".



