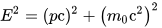The invariant mass can't change due to a net force. By a net force here I mean, a force that does work on the system. In SR it is often called a "pure" force (see robphy's answer for more details), and it corresponds to the Newtonian three forces we know from Newtonian mechanics.
For a point particle, it is very simple to see that such a force can't change its invariant mass. Consider the four momentum of such a particle:
$$ \mathbf{p} = \left(E, \vec{p} \right),$$
($c=1$ assumed here). So that, squaring this four momentum vector we just get, in agreement with the well known Energy-momentum relation:
$$ \mathbf{p}^2=-E^2+\vec{p}^2=-m^2, \tag{1}$$
where $m$ is the particle's rest mass. One can also easily verify this relation by putting $E=\gamma m $, $\vec{p} = \gamma m\vec{v}$, where $\vec{v}$ is just the ordinary three velocity of the particle, and $\gamma=\left(1-||\vec{v}||^2\right)^{-1/2}$.
So, applying a force to the point particle will not change $m$ as written in $(1)$.
If however, we have a system of two point particles (or more) and we compute its invariant mass by squaring the four vector sum of their four momenta, we get a quantity that in general may exceed the sum of the individual rest masses. Let's take the example of two particles:
$$ \mathbf{p}_i = \left(E_i,\vec{p}_i \right), \ (i=1,2) $$
\begin{align*}
\left(\mathbf{p}_1+\mathbf{p}_2 \right)^2 &= \mathbf{p}_1^2+\mathbf{p}_2^2+2\mathbf{p}_1\cdot\mathbf{p}_2
\\&= -m_1^2-m_2^2-2E_1E_2+2\vec{p}_1\cdot\vec{p}_2
\end{align*}
So if we set the above to be the mass squared of the compound system $-M_{\text{compound}}^2$, we find:
$$ M_{\text{compound}} = \sqrt{m_1^2 + m_2^2 + 2E_1 E_2 - 2\vec{p}_1\cdot\vec{p}_2}\ \ , $$
and it's not difficult to show that in general, it is always the case that $M_{\text{compound}} \geq m_1+m_2$. The rest masses of individual particles are still invariant of course, but we see that it's sensible to assign the compound system a mass that may exceed the sum of the individual rest masses.
This compound mass, as opposed to the mass of a point particle, can change. For example it will increase if energy is added to some part of the system, e.g. one of the particles absorbs a photon.
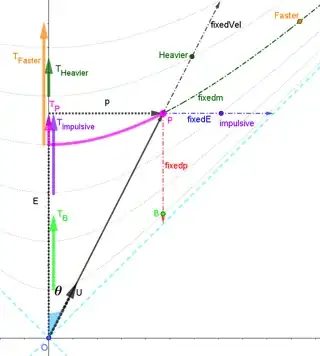
But, interestingly, a net force on this system, again will not change the invariant mass! To see why, consider again a system of two particles. Let's assume a frame where the system is initially at rest, and then a net force $\mathbf{f}_{\text{net}}$ acts for some time on the system's COM, accelerating it to some velocity $\vec{v}$. This can be described as follows:
$$ \underbrace{(m_1+m_2)(1,\vec{0})}_{\large\mathbf{p}_{\text{i}}} \stackrel{\large\mathbf{f}_\text{net}}{\longrightarrow} \underbrace{\gamma(m_1+m_2)(1,\vec{v})}_{\large\mathbf{p}_{\text{f}}}, $$
So we get, for the invariant mass after the action of the net force:
\begin{align*} \mathbf{p}_{\text{f}}^2 &= -\gamma^2(m_1+m_2)^2+\gamma^2(m_1+m_2^2)\vec{v}^2
\\&= -\gamma^2(m_1+m_2)^2\left(1-\vec{v}^2\right)
\\&= -(m_1+m_2)^2\left(\frac{1-\vec{v}^2}{1-\vec{v}^2}\right)
\\&= -(m_1+m_2)^2
\\&= \mathbf{p}_{\text{i}}^2.
\end{align*}
So all that's happening here, is that due to the action of the net force, we no longer have separate $E_1,E_2,\vec{p}_1,\vec{p}_2$. The entire system is accelerated to a shared velocity $\vec{v}$, and we see that as a result, only a single $\gamma$ factors out, like it does in the case of a single point particle, so that the invariant mass doesn't change from when the system was at rest. The same analysis is easily extendible to a system with any number of masses.
Furthermore, as long as the system is stable (doesn't radiate away energy in the form of EM waves, for example), this compound mass remains constant. Also, it is a Lorentz scalar as well, due to the added cross terms such as $2\mathbf{p}_1\cdot\mathbf{p}_2$ above being a dot product of four vectors. Hence the term "invariant mass" is still used, even when considering a system composed of many particles.
Also see related answer here by anna v.
Note that, it is possible to widen the scope of what we consider a force in relativity, to account for processes in which the rest masses change. Since by definition $\mathbf{p} = m\mathbf{u}$ we can write:
$$ \mathbf{f} = \frac{\mathrm{d}\mathbf{p}}{\mathrm{d}\tau} = \frac{\mathrm{d}m}{\mathrm{d\tau}}\mathbf{u}+m\frac{\mathrm{d}\mathbf{u}}{\mathrm{d}\tau}, $$
"Pure" forces mentioned above (that I call a net force here), are ones where the first term vanishes. Thinking geometrically about the worldline of the massive particle, we can see that only the second term induces a change to the four velocity $\mathbf{u}$ that's tangent to this worldline, because $\mathrm{d}\mathbf{u}/\mathrm{d}\tau$ is always orthogonal to the four velocity $\mathbf{u}$. So this means, this is the kinematic piece, that corresponds to "Newtonian" forces.
The other piece is often related as "thermal force" or "heat-like force". These types of forces don't do mechanical work, but can only increase/decrease the internal energy of the system. See for example "Special Relativity - Michael Tsamparlis" p. 325-329, 11.2, for a concise and clear explanation about thermal forces in SR, including a nice computational example given towards the end.