Electrostatic shielding using field lines isn't making sense

Question

I get that the E-field inside a conductor should be $0$ (inside meaning the empty space closed by a conductor AND the metallic part, like if you had a shell with inner and outer radii $a$ and $b$, $E = 0$ for $r<b$, even if you gave it some charge), because that is the only case that satisfies an electrostatic configuration, if there was an electric field anywhere (even in the empty spaces) it would mean there is an electric field in the metallic places (E field isn't discontinuous if there is no charge in it's way) which contradicts the condition that the systems configuration is electrostatic. This also implies that there is no charge inside a conductor, even a charged one because if there was, Gauss's law says there would be a flux and hence a field within the conductor which can't be so no charge enclosed either. That's fundamentally what a conductor is (correct me if I'm wrong though).

Now look at the following situation:

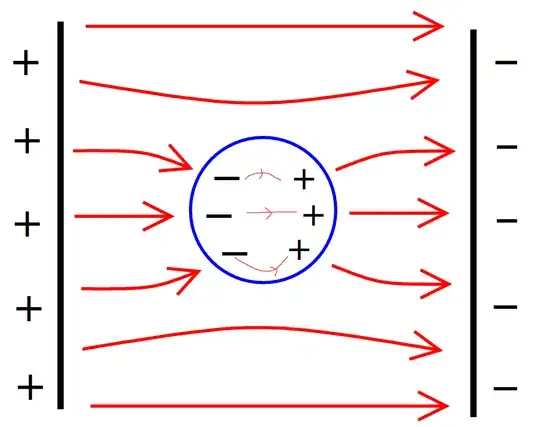
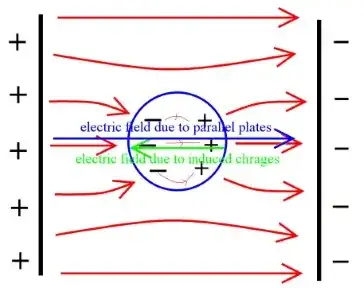
You have a neutral conductor held between two charged parallel plates. Now we say that the charges will redistribute themselves so that the above two conditions are met (they're sort of laws that conductors must obey), of which the more fundamental one is that $E$ in a conductor must always be $0$ which directly implies no $E$-field lines inside the conductor but if we trace the field lines, they will originate from the +ve charges on the left plate, some of which will go towards the sphere and some will terminate on the -ve charges on the right plate but the ones that do go towards the conductor ALL terminate on the -ve charges on the surface of the conductor, so no field lines due to the left plate in the conductor, same logic on the right hand side and you have a polarised conductor. Now there will be field lines running from the +ve to the -ve charges on the surface of the conductor too (just realised I drew them wrong), so in the end it seems to me that there is an E field inside the conductor (using this field line method).

I get that mathematically the net E field will look something like $E_{+ plate} - E_{-} + E_{+} - E_{- plate}$ and this will just cancel, but can someone do it using field lines.

Answer 1

There are two sets of charges producing electric fields as shown below.

• Electric field due to charges on parallel plates
• Electric field due to induced charges

Within the conductor those field are equal in magnitude and opposite in direction so the net field inside the conductor is zero.

Answer 2

The sphere in a uniform external field is a great problem, especially for understanding multipole moments: it's the 1st non-trivial moment, the dipole.

But the core of your post is not about shapes, it's about the field lines inside the conductor. This made me think: why add the extra problem of geometry, let's use a cuboid. A long and wide, but thin, cuboid. Basically: a conducting plate.

Your question about field lines and surface charges still stands, but everything is a straight line.

Now I can't draw a plot, so I am just going to make the plate infinite, which reduces the problem to 1-dimension.

Since the field from an infinite sheet is uniform, it doesn't not depend on distance, and I can put the source charges ($\pm\sigma$) at $x=\mp\infty$, so the field is:

$$ \vec E(x, y z) = \frac{\sigma}{\epsilon_0}\hat x \equiv +E_0\hat x $$

A uniform field everywhere.

Ok, bring in the conducting plate of thickness $D=2R$, centered at $x=0$.

The external field now leads to a surface charge density from the "left" (per drawing) side of the plate:

$$ \sigma_{\rm left} = -2\epsilon_0E_0 = -\sigma $$

and like wise on the right:

$$ \sigma_{\rm right} = +2\epsilon_0E_0 = +\sigma $$

Now if there were a figure, you would draw electric field lines connecting $-R$ to $+R$.

We can integrate Gauss's law as we move from Region I ($x \lt -R$ ) across the boundary to Region 2 ($-R\lt x \lt +R$).

In Region I, we have $E_0$ as the electric field.

The surface charge density:

$$ \sigma_{\rm left}(x, y, z) = \delta(x+R)\sigma_{\rm left} $$

causes a divergence in the field:

$$ \vec\nabla\cdot\vec E = \rho/\epsilon_0 $$

which reduces to:

$$ \frac{dE}{dx} = \sigma_{\rm left}\delta(x+R)/\epsilon_0 $$

which means as (I really should be at blackboard drawing this. I am basically trying to do that in narrative form):

$$ x_I \rightarrow x_{II} $$

$$ E_I \rightarrow E_I + (-E_0) = 0 $$

Drawing-wise, all the lines get gobbled up and the field is zero.

When you go to Region III, you cross the boundary and the positive surface charge density "restarts" the field.

So inside the conductor, to the left you see an infinite sheet of positive charge in the distance, and an infinite sheet of negative charge right there at $x=-R$ $\forall (y, z)$.

As you know, they cancel and the field is zero. (and same for charges on the right).

The only difference here with the conducting sphere is that you need Spherical Harmonics instead of constants to describe the charge densities that make it all happen.

Answer 3

You are thinking in terms of rules that charges and fields must obey. This is good, but thinking some slightly deeper rules might tell you why your rules must be obeyed and how to apply them correctly. You might have questions about why the deeper rules must be obeyed. Physics doesn't tell you why the deeper rules must be obeyed. They just are the way the universe works.

Point charges create electric fields. If you draw vectors, you see they all point toward or away from the charge. You can draw field lines that connect vectors. Those lines terminate or originate at the charge. The reason E fields to important is the force on a test charge is $F=qE$.

If you have two charges near each other, the E vectors at each point in space is the sum from each charge. You can calculate the force from the single summed E field, or you can calculate the forces from each field and add them.

Note that the field from each charge is not changed by nearby charges. The field lines continue radially inward/outward. However, the sum field does terminate/originate at each charge.

Pictures from Texas Gateway

If you sum the fields from point charges on parallel plate capacitors, you find a uniform field between the plates, and cancellation outside.

If you sum the fields for the induced charges in a wire, you find it looks a lot like a dipole.

You can treat the fields from the capacitor and wire the same way as from point charges. Each contains point charges. For each, the field it creates originates/terminates at charges in the part.

You can make a bigger system out of the parts. You can add the fields to find the field of the system. The total field originate/terminates on charges of the system.

---

Suppose you have a neutral conductor, full of electrons and protons. Each proton is surrounded by electrons. They each produce a field. But they all cancel. The total field is $0$.

Suppose have a charged capacitor and you put the wire inside. What happens?

The field from the capacitor goes through the wire. There is an E field inside the wire.

A conductor is a medium where charges can flow freely. If there is an electric field, electrons will be pulled toward the the positive plate. They will leave behind protons with too few electrons. Charges pile up on the sides of the wire. The piled up charges create a field in the opposite direction from the capacitor field. The sum inside the wire is weaker that without the wire.

As long as the field inside the wire is not $0$, there will be a force pushing electrons in a direction that weakens the field. This stops when the field is $0$.