Interpretation of geodesics in Kerr metric when approaching the event horizon

Question

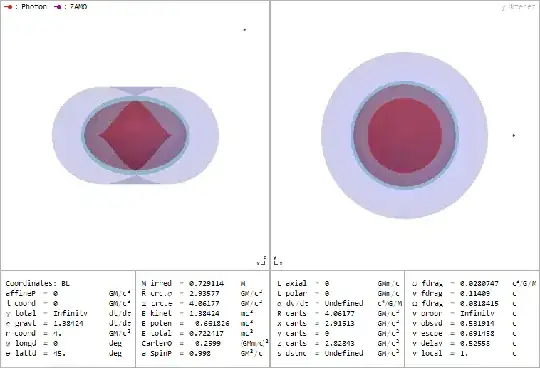
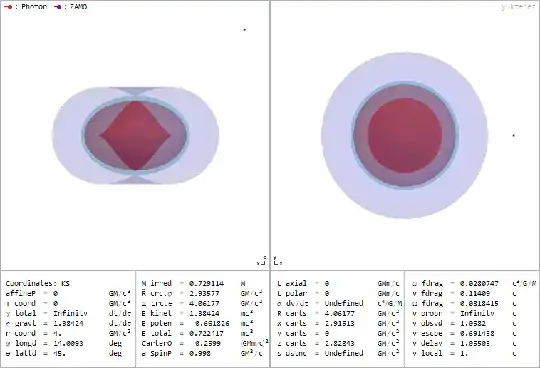
I'm learning about the Kerr metric and Kerr black holes from the book "General Relativity: An Introduction for Physicists, M.P.Hobson" and I'm interested in an interpretation for the equatorial geodesics. In the book it keeps saying that the $\phi$ and $t$ coordinates are "bad" coordinates. This is portrayed in the geodesics as $\dot \phi \propto \frac{1}{\Delta}$ and $\dot t \propto \frac{1}{\Delta}$ so as $r \rightarrow r_+,r_-$ the temporal and angular derivatives diverge. This is shown in the following figure in the book

Here I understand the behaviour of a free falling object from infinity, as the object approaches the outer event horizon, a far away observer would see the object orbit the black hole indefinitely and never go inside it. However, I don't understand why once it crosses the outermost event horizon the object would appear to rotate in the opposite direction and same with the time. It seems that the object would be rotating and moving through time in a negative direction. How can this be? Am I misinterpreting something?

Other than that, the book presents the Eddington-Finkelstein coordinates as a fix for these "bad" coordinates. Is there an easy way to derive the geodesics using this coordinate system? In this case what would the difference be between the new graphs and the ones shown here?

Lastly, in my general relativity course they made us use a code that numerically calculates the equatorial trajectories in a Schwarzschild black hole and we could see how using a far away point of reference a free falling object could never cross the event horizon but using the proper time the object crosses the horizon, can something similar be done for this metric?

Answer 1

Mikel Solaguren wrote: "In the book it keeps saying that the ϕ and t coordinates are "bad" coordinates."

I wouldn't call them bad, they just use the reference frame of an external observer.

Mikel Solaguren asked: "Other than that, the book presents the Eddington-Finkelstein coordinates as a fix for these "bad" coordinates. Is there an easy way to derive the geodesics using this coordinate system?"

It's as easy as deriving the geodesics in Boyer Lindquist or Doran Raindrop coordinates, just solve the geodesic equation as shown here at (11) (for the transformation see a/772647/24093).

Mikel Solaguren asked: "In this case what would the difference be between the new graphs and the ones shown here?"

Here is a photon falling into the black hole, in Boyer Lindquist coordinates where t is the proper time of the static bookkeeper at infinity it ends up corotating at the horizon:

while in Eddington Finkelstein style Kerr Schild coordinates where the timestamps are defined such that ingoing polar photons have dr/dt=-c it passes through the ring to exit into the negative space antiverse (assuming the maximal extension of an eternal black hole):

If you plot a circular equatorial orbit at constant r you won't see any difference though, that will of course stay circular in all coordinates.

Answer 2

This isn't a comprehensive answer (and also a bit too long to be a comment) because I'm only going to address the first question. While the object is orbiting the hole, it is affected by the curvature and also the angular momentum. The part of the figure to the right shows the object being increasingly affected by the angular momentum as it nears the event horizon. However, if a horizon gets crossed, the curvature takes over and the object (at rest) follows a unidirectional path unaffected by whether the angular momentum was greater or lesser. That is to say, inside the horizon, the time to arrival at the (in this case) ring singularity will depend only upon the mass of the hole.