A friend of mine has a homework question and we're having some trouble figuring out what physical mechanisms come into play for this.
An underwater swimmer sees a spherical air bubble that appears to have a diameter $d=$ 1.5 cm. What is its actual diameter?
We are having trouble, specifically, thinking of physical mechanisms that would change the apparent sizes of objects when seen underwater. Is it caused by refraction at the curved surface of the bubble?
Objects do appear larger (or equivalently nearer) underwater when wearing a mask or goggles. See the image below for confirmation of this fact. Why is this?
The interface between the water and your mask obeys Snell's law which can be written, in the small angle approximation, as $$ n_1\theta_1=n_2\theta_2. $$ Since air has an index of refraction of essentially 1 and water has an index of refraction of 1.33 the angle from which the rays of light reach your eyes is larger than the angle they would in air. This makes the angular size larger to your eyes which makes the object look larger relative to how they would look in air. This effect is shown qualitatively in the ray diagram below. The index of refraction of the glass interface does not play a role as long as 1) the thickness is much smaller than the distance to the object and 2) the two surfaces of the glass are parallel to each other.
You can get an approximate answer as to how much larger things would look by assuming that the distance between your mask and the object is much larger than the distance between the mask and your eyes. In this case the angle which the ray hits the mask from is roughly the same as it would be in air, and the angle it hits your eye with is simply $n_2/n_1=1.33$ times that. So, the approximate magnification is 1.33 in water. For objects which are closer up you would need to relax the small angle approximation as well as take the distance between the mask and your eyes into account.
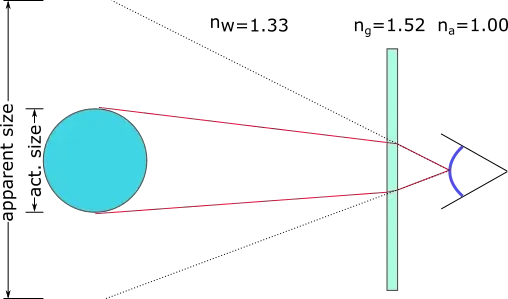
Qualitatively, the thing that happens under water (when you wear a diving mask) looks like this:
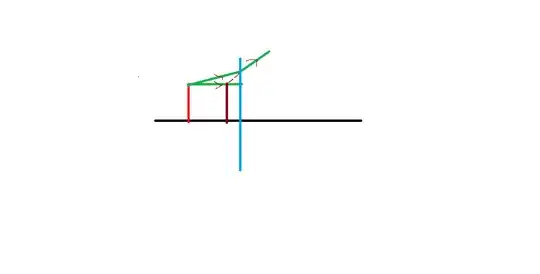
The green lines represent the path the light would have taken without the water, and therefore the "apparent size" of the bubble. But as you can see, the refraction of the light away from the normal (transitioning to a medium of lower refractive index) causes the angle at which the light appears at the eye to change - and since the angle subtended by the object is larger, it "appears" larger (for the given distance).
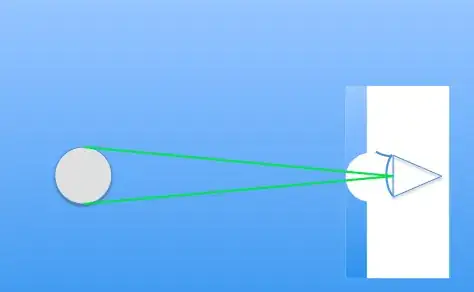
Goggles that are slightly curved (with the center of curvature at the lens of the eye) prevent this from happening - it's almost as if you had put a lens with a negative focal length on the inside of your goggles:
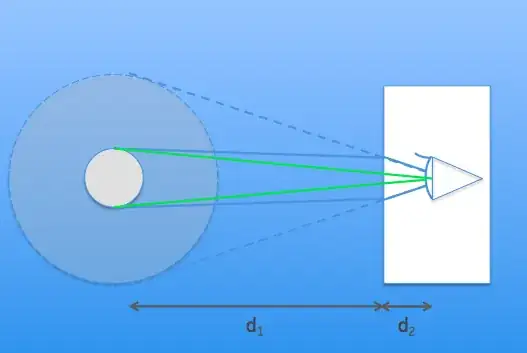
Mathematically, if $d_1 \gg d_2$ and the diameter of the bubble is much less than the distance to the goggles, you can deduce the change in angle straight from Snell's Law, and conclude the bubble is $n_{water}$ greater than it would be if observed "normally". Since it is observed to be 1.5 cm, we conclude its real size is 1.5/1.33 = 1.1 cm (25% smaller).
The presence of glass (N~1.5) between the water and the air inside the goggles doesn't change the answer - because if we call the intermediate refractive index $n_i$ and the intermediate angle $\theta_i$, we can write Snell's Law in two parts:
$$n_w \sin\theta_w = n_i \sin \theta_i = n_a \sin \theta_a$$
Leaving out the bit in the middle, you see that the refractive index of the glass does not, in fact, affect the magnification. But the curvature of the glass does - very much.
Just as you can think of the curved goggles (my second diagram) as "correction" for the magnification (as you know, lenses with negative focal length make things look smaller), so you can consider the original situation as a "positive" lens - since, depending on their path, the rays traverse a different amount of water. I am struggling a bit to find a good way to represent that graphically - but it's basically the counterpoint to the second diagram above. And having a positive lens in the path causes magnification, of course.
If the "underwater swimmer" in the question was not wearing goggles, he/she would have a hard time focusing on the bubble (since the refractive power of the eye mostly comes from the interface of the cornea and the air - replace the air with water and you have a very poor lens).
If you could see properly with your eyes under water (you had some amazing internal lensing mechanism) you would see the bubble with its usual angular size. Wondering how big it is, you could bounce a LIDAR signal off the bubble and deduce, from the round trip tipe, how far away the bubble is. Under water, that signal would take $n_w$ times longer than in air. So if the same angular size appears to be further away, you once again conclude that the bubble is $n_w$ times larger than it really is.
Objects in water, seen through a flat surface, do appear magnified when the eye is close to the surface. Anyone who has used a diving mask under water will be aware of this.
When the flat water surface is close to the eye, then rays entering the eye at an angle have passed through the air/water interface and have been refracted towards the eye. This increases the included angle from the perceived object and hence it appears larger. If the eye is a long way from the interface, then the light rays entering the eye pass at nearly the same angle through the interface and so there is little difference in the amount of refraction.
The size of the image itself doesn't change. However, because the image looks closer than the object, you can have the feeling that the object is closer. Take a look a the following picture to understand it better. In red, it is drawn the object. In green, it is drawn the rays of light. The image is in a darker red. A blue line is the water surface.
This is for a flat water surface. If the surface was curved, seeming convex in relation to you (like a spherical aquarium), then indeed the size of the image would be bigger!
If we see in water and put objects like pencil, pen, etc. You will see an magical effect or magical phenomenon occurs in water that the object looks larger from when it is in diminished size or form because the water has refractive index 1.333 or the main thing to notice or main point is that the water acts or works like lenses that magnifies the image or water droplets acts like an concave or convex mirror both to see the objects size much larger than its actual position... When we see the object larger in size when it is in water the image is apparent , virtual not real in the water. And we have notice sometimes why is the object seems blurry, illusory in water? The answer is the illusory attenuation of light or blurry vision is because of our eyes wrong focus between our eye or to in the water .. This is also called blurry vision of object or underwater vision object seems blurry because when our rays go into the water they bents and thus resulted in incorrect or wrong angle.. This is also because when you swims under water the things became blurry because our eyes swollen with salt that is neutral I think.. Made up of sodium elements... That's the full reason.
