Limit of relative speed

Question

Let us suppose that two rockets travel in opposite directions from the earth. The speed of each is more than half the speed of light. My question is whether the two rockets will travel at more than the speed of light relative to each other.

Answer 1

Indeed this is one of the most widely answered basic question, but in the domain of answers, there's always room for improvement.

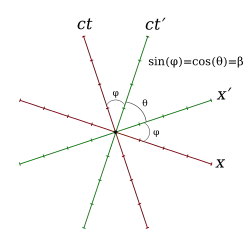
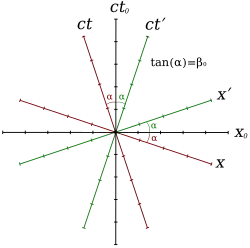
So wikipedia covers this in its Loedel Diagram section on Minkowski diagrams (https://en.wikipedia.org/wiki/Spacetime_diagram).

If we start with two object moving (at any speeds, in any directions), there its going to be a transformation to a new frame, the Median frame, $S_0$ which is your original "rest" frame. For reference, we say this is Alice's frame. In this frame, the objects are moving at $\pm\beta$ in the $x$-direction. (I chose $x$, because the original 3D space situation has been reduced to a 1D problem).

For clarity, we can call the frames $S_{\pm}$ and assign them to Bob and Charlie, for reference. (Note: I think it's important to be specific and follow a consistent protocol when addressing SR problems...such diligence will payoff in the long run. This is a view that I developed after years of reading questions on this site).

So now we can restate your OP: Suppose Alice is at rest ($S_0$), and she sees two equidistant spaceships (Bob and Charlie in $S_+$ and $S_-$, respectively) moving away from her at $v_{0, +}=+\beta$ and $v_{0, -}=-\beta$, aka $\pm v_0$. [Note: I specified "equidistant" so that all frames share a common origin:

$$ O = (0, 0)_0 = (0, 0)_+ = (0, 0)_- $$

where I have introduced standard Minkowski diagram coordinate $(t, x)_{\rm Frame}$ that unambiguously give time and space coordinates in a labeled "Frame". I also introduced a notation:

$$ v_{{\rm Frame}, {\rm object}} $$

which a concise way of describing "The velocity of object in frame, e.g. $v_{0, +}\equiv v_{\rm Alice, Bob}$ is the speed of Bob in Alice's frame. ]

Now we can reframe the question: Instead of, "What is the limit of relative speed?", it's, "What is $|v_{+,-}|$?" (or, by symmetry, $|v_{-, +}|$).

Now that's the title question. In the body, you specify $\beta=\frac 1 2$...idk, I'll do the general case. The fact that I started with any two random velocities $\vec v_{\pm}$, which of course must be satisfy $|\vec v_{\pm}| < c$, and then asserted a median frame (Alice) exists where $v_- = -v_+$ you should anticipate that $|v_{-, +}| < c $.

Anyway, back to wikipedia and it's Loedel diagrams:

[Note: apologies for ($0$, primed, unprimed) in the figure, while I call them ($0, +, -$) in the text; that is an artifact of figure-scavenging]

So if we're looking for $v_{+, -}$, the speed of Charlie in Bob's frame, well, Charlie's world-line is the $t$ axis, while Bob's is the $t'$ axis in the figures. It should be clear that as $|v_{\pm}| \rightarrow c$, the $t$ axis approaches -45 degrees from vertical (Remember, $c$ is constant in all frames, which means the $\pm 45^{\circ}$ lines, aka: the light cone, is fixed in all frames).

So the answer to the titular question is $c$, and that is strictly a limit, we are never getting there.

The math works out such that:

$$ v_{\pm, \mp} = \frac{v_{0,\pm} + v_{0, \mp}} {1 + \frac{v_{0,\pm}v_{0, \mp}}{c^2} } = \mp \frac{2v_0}{1 + v_0^2}$$

which, for $v_0 = \frac c 2$ gives $0.8c$.

The signs work out so that Bob see's Charlie moving to more negative $x_+$, while Charlie sees Bob moving to more positive $x_-$.

On a final note: while velocities do not add linearly, rapidity:

$$ \omega \equiv {\rm arctanh}(\beta) $$

does.