I'm currently taking a GR course and, as we were studying the Schwarzchild solution, we discussed how someone entering a black hole (Alice) could pass through the event horizon in finite proper time, while taking infinite coordinate time according to an observer (Bob). Then the question was posed, if Bob always sees Alice outside the horizon, could he send a signal to Alice at an arbitrarily late time and have Alice receive it before she crosses the event horizon? My professor responded that no, Bob would also see the signals slow down as they approached the event horizon, and some of them would slow down fast enough to never (according to Bob) reach Alice. I wasn't completely satisfied by this answer, so I wanted to approach it quantitatively.
The question: Alice free-falls into a Schwarzchild black hole from infinity (her motion is completely radial, $\frac{d\theta}{dt} = \frac{d\phi}{dt} = 0$, and her velocity is $v = 0$ at $r = \infty$). When she passes $r_{A_0}$, Bob, located at $r_{B_0}$, sends a beam of light radially inward toward Alice. What is the beam of light's position, $r_B$, as a function of Alice's position, $r_A$?
My approach: For massive particles, the equation of motion around a Schwarzchild black hole is
$$\left( \frac{dr}{d\tau} \right)^2 + \left(1 - \frac{R_s}{r} \right)\left(\frac{L^2}{r^2} + 1\right) = E^2.$$
From our assumptions, $L = 0$ and at infinity, $E = 0 + (1 - 0)(0 + 1) = 1$, so this just becomes
$$\left(\frac{dr}{d\tau} \right)^2 + 1 - \frac{R_s}{r} = 1 \\ \left(\frac{d\tau}{dr} \right)^2 = \frac{r}{R_s},$$
and plugging this into the Schwarzchild metric yields
$$-\frac{r}{R_s} = -\left(1 - \frac{R_s}{r} \right)\left(\frac{dt}{dr} \right)^2 + \left(1 - \frac{R_s}{r} \right)^{-1} \\ \frac{dt}{dr_A} = -\sqrt{\frac{r_A}{R_s}}\left(1 - \frac{R_s}{r_A} \right)^{-1}.$$
On the other hand, for a massless particle we have the equation of motion
$$\left( \frac{dr}{d\lambda} \right)^2 + \left(1 - \frac{R_s}{r} \right)\left(\frac{L^2}{r^2}\right) = E^2,$$
which immediately gives
$$\frac{dr}{d\lambda} = -E,$$
taking the negative branch since we want radially inward motion. We also know the conserved quantity $E$ is defined $E \equiv \frac{dt}{d\lambda} \left(1 - \frac{R_s}{r} \right)$, so
$$\frac{dt}{d\lambda} = E \left(1 - \frac{R_s}{r} \right)^{-1},$$
and dividing these two gives
$$\frac{dt}{dr_B} = -\left(1 - \frac{R_s}{r_B} \right)^{-1}.$$
Diving this with our expression for $\frac{dt}{dr_A}$ gives us the final expression
$$\frac{dr_B}{dr_A} = \sqrt{\frac{r_A}{R_s}} \left( \frac{r_A}{r_B} \right)\left( \frac{r_B - R_s}{r_A - R_s} \right).$$
This can be solved with separation of variables, so at this point I just plugged what I had into Mathematica and got 
$$r_B(r_A) = R_s \left(W_0\left(\frac{(r_{B_0}-R_s) \exp \left(\frac{2 r_A^{3/2}+6 R_s^{3/2} \left(\tanh ^{-1}\left(\frac{\sqrt{r_{A_0}}}{\sqrt{R_s}}\right)-\tanh ^{-1}\left(\frac{\sqrt{r_A}}{\sqrt{R_s}}\right)\right)+6 \sqrt{r_A} R_s-2 r_{A_0}^{3/2}-6 \sqrt{r_{A_0}} R_s+3 \sqrt{R_s} (r_{B_0}-R_s)}{3 R_s^{3/2}}\right)}{R_s}\right)+1\right).$$
But this doesn't behave as I would expect — we have the strange feature that $r_B(R_s) = R_s$, which seems to imply that Alice will always intersect the light beam at the event horizon. I also plotted $r_B(r_A)$ against $r_A$ for several values of $r_{A_0}$ and $r_{B_0}$, and it seems like even in the cases where $r_{B_0}$ is significantly greater than $r_{A_0}$, it rapidly drops to meet $r_A$ near the event horizon: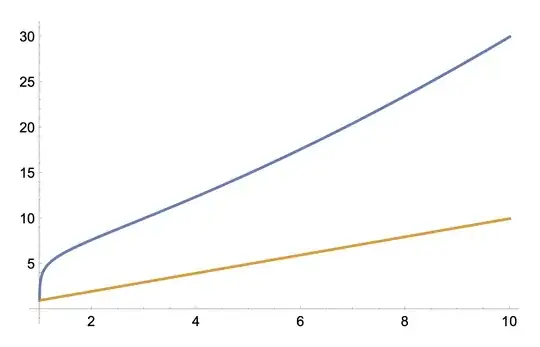
Above I have $y(r_A) = r_B(r_A)$ (in blue) plotted against $y(r_A) = r_A$ (in orange), for $R_s = 1$ and initial values $r_{A_0} = 10$ and $r_{B_0} = 30$. The behavior becomes even more extreme when $r_{B_0}$ is, say, 100:
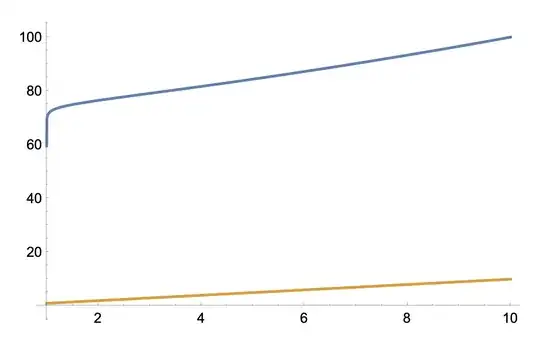Here it seems like the beam won't reach Alice in time, but just before she crosses the event horizon it rapidly speeds up to meet her (so much so that Mathematica doesn't even have the numerical precision to fully render the plot).
Now I'm wondering exactly what I did wrong, because my professor (and everywhere I've looked online) says that there are some values of $r_{A_0}$ and $r_{B_0}$ for which we should have no intersection points. My final function also just doesn't seem to make much sense, since it seems like there should be some values for which $r_B(R_s) < R_s$, to signify the beam of light making it to the black hole before Alice. But even when $r_{B_0} < r_{A_0}$, the beam of light seems to slow down so that it meets Alice at exactly $R_s$. I don't need someone to do out the entire computation, but I would like to know where I went wrong and get a little guidance on what I can do to fix my equation. Thanks!
