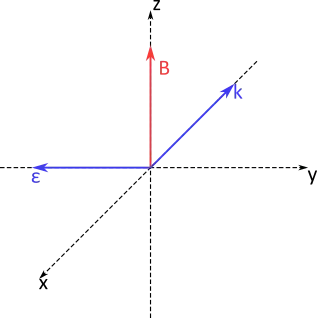
I am trying to understand how an atomic transition between different Zeeman sub-levels can happen when the propagation direction of the light driving the transition is perpendicular to the magnetic field defining the quantization axis. In particular, something like this
I am aware that this question is quite related to this one, but I am looking for a more in-depth explanation of what happens in this situation (case three of the picture on the post I am referring to), or more appropriately, I want to know if my reasoning is sound.
So, to start the setup of this situation, I am interested in a transition of the form $$\left|g\right>=\left|n,l=0,m=0\right>_{z}\to\left|e\right>=\left|n^{\prime},l^{\prime}=1,m^{\prime}=1\right>_{z},$$ for instance (the $z$ subscript is to indicate that the quantization of angular momentum is along this axis). The Hamiltonian that drives this transition (in the dipole approximation) would read something like $$\hat{H} = -e\hat{\mathbf{r}}\cdot\hat{\mathbf{\epsilon}}E_{0}\cos(\omega t),$$ where $\hat{\mathbf{r}}$ is the position operator, and $\hat{\epsilon}$ is the polarization vector of the light field. In spherical coordinates, the polarization of the light field (along the $y$ direction only, as it is linearly polarized) would be written as $$\hat{\epsilon}_{y}=\frac{i}{\sqrt{2}}(\hat{\epsilon}_{-1} - \hat{\epsilon}_{+1}).$$ (I am taking the decomposition in spherical coordinates from eq. 4.110 from Bransden & Joachain's "Physics of Atoms and Molecules", 2nd ed). Then, the corresponding Rabi frequency of the transition I am interested in would be $$\left<e|-e\hat{\mathbf{r}}\cdot\hat{\epsilon}|g\right> = -e\mathbf{r}_{eg}\cdot\hat{\epsilon} = -e\sum_{q=0,\pm 1}\epsilon^{*}_{q}[\mathbf{r}_{eg}]_{q} = e\frac{i}{\sqrt{2}}(I^{+1}_{n,0,0;n^{\prime},1,1} - I^{-1}_{n,0,0;n^{\prime},1,1}),$$ (from eq. 4.112 in B&J) where $I^{q}_{n,l,m;n^{\prime},l^{\prime},m^{\prime}}$ is the matrix element of the position operator between the two states, $\left|n,l,m\right>$ and $\left|n^{\prime},l^{\prime},m^{\prime}\right>$. Then, according to the selection rules resulting from this integral, for $q=+1$, then only $I^{+1}_{n,0,0;n^{\prime},1,1}$, where $\Delta m=+1$ (and $\Delta l=+1$) holds, is different from zero.
Then, my conclusion is that, if $\Omega$ is the Rabi frequency for the same type of transition when $\mathbf{B}\parallel\mathbf{k}$, then the Rabi frequency for this case, name it $\Omega^{\prime}$, would be $$\Omega^{\prime} = \frac{i}{\sqrt{2}}\Omega.$$
Is this reasoning correct?