0

The picture above is from David Morin's book Introduction To Classical Mechanics page 371

The picture above is from David Morin's book Introduction To Classical Mechanics page 371

I couldn't comprehend what he meant by motion like

Would I be able to find velocity of any point if I know translation velocity of any point say P and $\omega$ angular velocity of axis passing through P?

Also I have seen people using this theorem on CENTER OF MASS but why on it why not some other point ?

EDIT

Below I am attaching another picture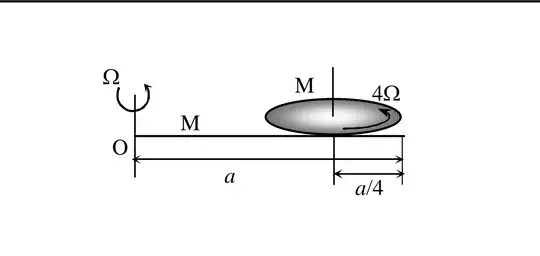question on rotation

In diagram all information is given and the shaded shape is circular disk and consider rod massless now I want to know

How would I do apply this theorem if I wanted to find angular momentum of body ($\alpha$) taking point P to be left end of the disk not the Centre Of Mass Of Disk

Harshit Gupta
  • 11

3 Answers3

1

Since the body is a rigid body, the distance between any 2 points of the body is constant.

Now if we were to take a reference frame positioned at P, the only way that the other points on the body would move is in circles around a axis that passes through P. Any other motion changes the distance between the points

This essentially proves the theorem that the velocity at any point can be written as the sum of translational motion of P and the rotational motion about a axis passing through P.

Dev Not Taken
  • 1,127
0

I would add some calculations to @DevNotTaken answer. Imagine that you have a point $P_1$ in the position $\vec R_1$ and another arbitrary point $P_2$ with position $\vec R_2$. By definition, the position of $P_1$ relative to $P_2$ is $\vec r = \vec R_1 -\vec R_2$ and the distance between the points is the modulus $r=|\vec r|$. Now, if we use the point $P_2$ as a reference frame, we could use polar coordinates to write $\vec r = r\hat r$, where $\hat r = \hat r(\theta,\phi)$ is the unit vector pointing from $P_2$ to $P_1$ and it depends on the polar coordinates. Now, we write

$$ \vec R_1 = \vec R_2 + \vec r $$

To calculate

$$ {d \vec R_1\over dt} = {d\vec R_2\over dt} + r {d\hat r\over dt} $$

where I used the fact that the distance $r$ does not vary on time, which is true if the two points relies in a rigid body. I think you can convince yourself that the last term is an angular velocity and there is a whole theory to describe it properly. The left hand side is the velocity of the point w.r.t the starting origin and the first term on the right hand side is the velocity of the coordinate in the body.

Ruffolo
  • 4,397
0

According to Michel Chasles' theorem, any arbitrary movement of a rigid body can be represented by a screw motion. In this motion, the body rotates around the instantaneous axis of rotation and simultaneously translates in the direction of this axis.

thus, for a given angular velocity $~\vec\omega_{0K}~$ and the velocity $~\vec v_{0S}~$ at the center of mass, you obtain the velocity at point P $$\vec v_{0P}=\lambda\,\vec\omega_{0K}\quad,\lambda=\frac {\vec\omega_{0K}\cdot\vec v_{0S}}{\vec\omega_{0K}\cdot \vec\omega_{0K}}$$

and the distance to the instantaneous axis of rotation.

$$\vec r_{SP}=\frac{\vec\omega_{0K}\times\vec v_{0S}}{\vec\omega_{0K}\cdot \vec\omega_{0K}}$$

where $~\vec r_{SP}\perp\vec\omega_{0K}$

Prof. Dr.-Ing. G. Rill

Script: Prof. Dr.-Ing. G. Rill

Eli
  • 13,829