If the height difference between the mercury level in the two arms is $h$ (it's called $\Delta h$ on the figure), then
$$P_1 - P_2 = h\rho g$$
where $P_1,P_2$ are the pressures in both wings (called $P,P_{\rm ref}$ on the figure). One of them is the measured atmospheric pressure. The two pressures are being subtracted because the air pushes the liquid from the two sides in two opposite directions. You may also move $P_2$ to the right hand side, so that the two sides exactly express the pressure in both directions (to be specific, you may think about forces acting on a special separator inserted to the point $B$ at the bottom of the figure - most of the mercury cancels, only the height difference doesn't).
The basic-school formula $h\rho g$ for the pressure may be derived as the force of the mercury column per unit area of the base. The mass is $V\rho = A h\rho$, the force is $g$ times larger i.e. $A h \rho g$, and the force per unit area is therefore $h\rho g$ because $A$ cancels. My derivation is only valid for "cylindrical" shapes but the $h\rho g$ formula is actually true for any shape - the pressure only depends on the depth $h$ beneath the surface.
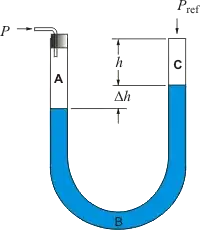
Restricting our attention to the pressure and height differences only, it's clear that $h=1$ millimetre of mercury corresponds to the pressure difference:
$$ \delta P = h \rho g = 0.001 \,{\rm m} \times 13,595.1\, {\rm kg}/{\rm m}^3 \times 9.80665\,{\rm m}/{\rm sec}^2 = 133.332 \,{\rm Pa} $$
The inverse relationship is 1 Pascal is equivalent to $1/133.332 = 0.0075006$ mmHg. The exact values of the densities are a little bit conventional - the densities depend on temperature and pressure and the gravitational acceleration depends on the place. In the past, 1 mmHg wasn't needed that accurately. In the modern era, we define 1 mmHg by your relationship, and 1 Pa is much more accurately defined in terms of "fundamental physics".
