-3

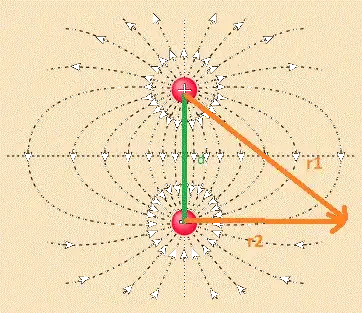
It is well known fundamental behaviour that, oppositely charged bodies attract each other (I don't know whether it applies also for charges of equal magnitude or not), and identical charges repel each other.

It is also well known that, a system of oppositely charged bodies with equal charge in magnitude, has zero net charge.

If a system has oppositely charged bodies, with equal charge in magnitude, it would imply that, there will be zero net charge, and the vector field's had got cancelled each other, like around a current carrying conductor, there is no electric field because, charge on current carrying conductor is zero, as one electron enters the conductor, the other will be leaving the conductor. Now, if there is no field, how could the oppositely charged bodies (of equal charge in magnitude) attract each other, they should not feel any force, isn't?.

Taking into account all the above statements, would it imply that, two oppositely charged bodies (of equal charge in magnitude) attract each other?

[All statements made, are up to my view. Any correction advisory is welcome]

LINKS

Community
  • 1
Sensebe
  • 5,889

1 Answers1

3

Taking into account all the above statements, would it imply that, two oppositely charged bodies (of equal charge in magnitude) attract each other?

Yes. Two opposite charges will always attract, independently of their magnitudes. That's what Coulomb's law says: $F=\dfrac{kq_1q_2}{r^2}\implies F=-\dfrac{k|q_1q_2|}{r^2}$. If they are equal in magnitude: $F=-\dfrac{kq^2}{r^2}$

If a system has oppositely charged bodies, with equal charge in magnitude, it would imply that, there will be zero net charge, and the vector field's had got cancelled each other

No. Total net charge doesn't mean zero field, because there is some separation $d$ between the charges.

The field for an individual charge is: $E=\dfrac{kq}{r^2}$.

And the superposition principle states that fields add up: $E_{\mathbf{total}}=E_1+E_2$.

This means that, if we have two opposite charges of equal magnitude:

$$E_{\mathbf{total}}=E_1+E_2=\frac{kq}{r_1^2} - \frac{kq}{r_2^2}$$

Unless $r_1=r_2$ is zero (that is, $d=0$), $E$ will never be zero. Intuitively, you can think that each field tries to cancel, but they can't because there is some displacement. The smaller the distance between the charges, the cancellation will be better. If the charges are largely separated (one charge here and other in the Moon), you would have two independent fields.

See for example the field of a dipole:

enter image description here

jinawee
  • 12,675
  • 7
  • 60
  • 102