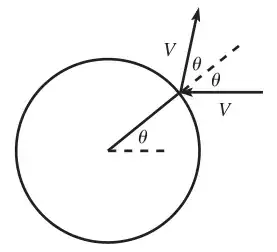
I am exploring the dynamics of a particle colliding with a cylindrical surface at an angle θ. A particularly intriguing aspect of this scenario is how the particle "knows" about the surface curvature during the collision. This raises fundamental questions about the nature of the interaction.
When a particle approaches a cylindrical surface, it impacts at a specific angle, resulting in a deflection rather than a simple reversal of direction. This behavior suggests that the particle interacts with the curvature of the surface in a way that is not merely a random event. Instead, the angle of impact and the resulting motion appear to depend on the geometric properties of the cylinder.
From a microscopic perspective, the collision occurs at the atomic or molecular level, where forces between the particle and the surface come into play. However, I wonder how this microscopic interaction translates to a discernible response to the curvature of the surface. Is the particle's deflection purely a consequence of momentum and energy conservation, or is there a more fundamental principle at work?
Additionally, I would like to understand whether this curvature interaction is purely a microscopic phenomenon or if macroscopic properties, like the shape of the surface, significantly influence the collision outcomes. Are there specific theoretical models or frameworks that can explain how particles respond to curved surfaces?