Help understanding Feshbach resonance

Question

Currently this is my understanding of feshbach resonance, I know that free unbound atoms are coupled to a molecular state in which the atoms are tightly bound. The closer this molecular level lies with respect to the energy of two free atoms, the stronger the interaction between them. I know we can use a magnetic field to shift the energies of two free atoms relative to the molecular state and thereby controls the interatomic interaction strength. But how exactly is this done? I understand it probably has something to do with the zeeman shift but is anyone able to provide me with a more intuitive explanation as to what is actually happening?

Answer 1

Consider the elastic collision of two atoms. By separating the center-of-mass and the relative motion of the atoms and by transforming into the center-of-mass frame, the scattering process is described by the motion of a single particle in a 2-body interaction pseudo-potential $V(r)$. In this picture the single particle represents the relative wavefunction of the two atoms.

Semi-classically it is intuitively clear that changing the pseudo-potential depth changes the kinetic energy of the particle inside the well. Therefore, the interaction time (the time the particle spends inside the potential well) depends on the depth of the pseudo-potential. If the energy of a bound-state matches the kinetic energy of the incident particle, the particle transforms all its kinetic energy into potential energy. It stops inside the potential, the interaction time becomes infinite. However, if the energy of the bound-state slightly mismatches the kinetic energy, the ”velocity” of the particle inside the potential strongly depends on the sign of the mismatch: If $E_{bound} \lt E_{kin}$ the velocity is small, while for $E_{bound} \gt E_{kin}$ it would be huge, because the bound-state is out of reach. Thus, the interaction time of the particle is influenced by the last bound-state inside the potential well. Therefore, small changes in the potential may tremendously change the scattering length.

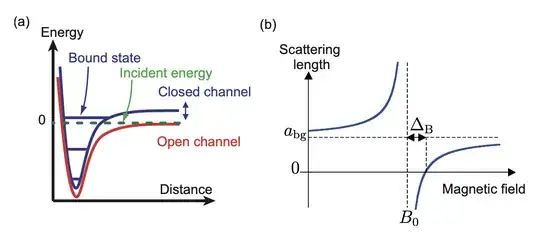(a) The coupling between two molecular potentials allows to tune the scattering length. Whenever a bound-state matches the kinetic energy of the colliding atoms, a Feshbach resonance appears in the scattering length. (b) Behaviour of the scattering length in the vicinity of a magnetic Feshbach resonance, with width $\Delta B$ and position $B_0$.