Deriving Faraday's law from a special case, do we consider Lorentz force on electrons only or Laplace force to derive it?

Question

In this electromagnetism class, professor derives Faraday's law from a very specific case (he specifies Faraday's law is a kind of axiom in physics, but that in this very special configuration, one can "derive" it).

The configuration is: we have a zone where there's a constant magnetic field going out of the screen, a closed circuit is half immersed in this zone and someone is pulling the circuit out of the zone (towards the right) with a velocity $\vec{v}$.

Professor computes the Lorentz force on the electrons of the left leg of the circuit (there's no $\vec{E}$ term in the Lorentz force, since we are in magnetostatics). After integrating it over all the circuit, he finds $hBv$. 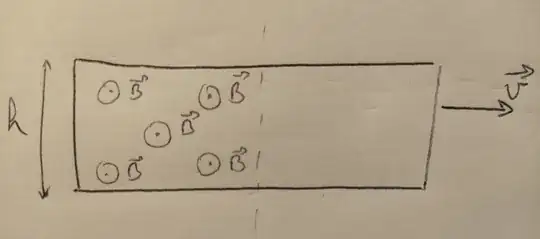Similarly he finds that $$-\frac{d\phi_B}{dt} = hBv $$ .

My question is: why didn't he also consider the Lorentz force on the cations of the left leg (they are moving too)?

Said slightly differently, I'm wondering whether we should consider the Laplace force for the term traditionally on the left-hand side of the Faraday's law or consider solely the Lorentz force on negative charge carriers?

My understanding of the Laplace force is that in this case, the Laplace force term due to the electrons cancels out with the Laplace force term due to the cations (because of charge neutrality).

So to sum up either the LHS of Faraday's law concerns the Laplace force (in this case there is no way to derive Faraday's law from any special configuration), either we consider only the Lorentz force of the negative charge carriers in Faraday's law (this possibility seems dubious, why would negative charge carriers be given such a special treatment?).

EDIT:

My understanding of this situation is that the changing magnetic flux creates an EMF, which in turn creates a current (some would call it induced current), which from Laplace force exerts a force on the circuit towards the left (opposing the pulling force "someone" exerts on the right). But in no way (from my opinion) this configuration allows us to "derive" Faraday's law.

Answer 1

Motional emf in a circuit, which is EMF due to motion of the circuit in magnetic field, is defined as

$$ \mathscr{E}_{motional} = \oint_{circuit} d\mathbf s \cdot (\mathbf v \times \mathbf B_{ext}), $$ where $\mathbf v$ is velocity of the conductor. Note, this is not velocity of the mobile charge, which we can denote as $\mathbf v + \mathbf u$, where $\mathbf u$ is velocity of the mobile charge in the frame of the conductor. For this reason, the expression $\mathbf v\times \mathbf B_{ext}$ is not magnetic force per unit charge, acting on the mobile charge in the conductor. So it is not the magnetic part of Lorentz force acting on the mobile charge; that force, per unit charge, would be

$$ \mathbf f_{Lorentz} = \mathbf v\times \mathbf B_{ext} +\mathbf u\times \mathbf B_{ext}. $$

It turns out that EMF defined the above way contributes to net EMF driving current in the circuit, in the sense of Kirchhoff's second circuital law, so it is a good definition.

Your professor aims to demonstrate that motional EMF defined this way also equals change of magnetic flux through the circuit due to its motion, and thus so-defined motional EMF also obeys Faraday's law in its original formulation (minus rate of change of magnetic flux equals EMF in the circuit).

The demonstration/proof does not involve the Laplace force at all; the Laplace forces would be present in the experiment, but they act on the wire elements, not on the mobile charge, so they do not contribute to EMF. The Laplace force acting on the vertically drawn element in magnetic field, moving to the right, has magnitude $$ |F_{Laplace}| = B_{ext}IL, $$ where $L$ is length of the element; and its direction is opposite to that of velocity $\mathbf v$.

Notice the formula for the Laplace force does not contain velocity of the conductor $\mathbf v$; this force does not depend on velocity of the conductor, it acts even if the conductor is at rest. The Laplace force depends on electric current $I$ in the conductor.