There is mathematics in physics but is there any physics in mathematics?

Question

Are there situations where physics is needed to solve mathematical problems? While it's well-known that many problems in physics require mathematical techniques for their solutions, I wonder if there are scenarios where a solid understanding of physics principles is necessary to tackle certain mathematical problems.

Answer 1

Are there situations where physics is needed to solve mathematical problems?

No.

And the reason is simply that mathematics is complete in and of itself. Indeed mathematicians would not accept a physical argument to "solve" a problem and would require a purely mathematical proof to accept a proof.

Now physics does provide some problems for mathematicians to develop a valid proof for, and physics also provides real world limits that can lead to classes of solutions that are valid only within those limits (e.g. specific boundary limits, specific domains for valid parameter values, specific symmetries that are required). However, that just leads to specialist solutions to more general formulations of problems. It does not solve the problem.

Physics can provide an intuition for the form of the solution or an approach to it, but not the actual solution.

In general pure mathematicians often find the mathematical rigor of physicists sorely lacking. We'll take short cuts, because we know it works out, which a mathematician cannot do, or to put it another way, doing that in mathematics would get you half marks at best. I remember being very criticized by some mathematicians for providing a very physics-like interpretation of a problem which I think most physicists would accept as perfectly reasonable.

Mathematics is an entirely self-contained world.

They don't need us, but we do need them.

Possibly best to end with a note from Xkcd.com on scientific purity.

Or maybe I should have started with that.

Answer 2

I would like to add on top of @StephenG's great answer, that even if physics is not necessary to solve mathematical problems (although it might sometimes help), it has proven crucial to find the problems. Indeed, physics has motivated many areas in mathematics, although initially in a less formal (or more physicist) way. The classic example is calculus, whose invention has been tied deeply to the development of mechanics, which requires the ideas of calculus and ODEs. Other examples can be found in the theory of PDEs, where some of the most important equations like Fourier's were discovered while studying heat transfer, and it's solution gave birth to Fourier series.

TLDR: Even if there's no physics in maths, physics can inspire or motivate lots of mathematics!

Answer 3

Although algorithms for pseudorandom number generation have become highly sophisticated, sometimes real random numbers are required. In such cases, hardware random number generators based on physical phenomena like electric noise at a junction are the basis for the mathematical solution of the problem.

In general, analog computers exploit Physics to model the solution of many different mathematical equations.

[joking mode on]

Pushing the last sentence to its limit, one could even say that every solved mathematical problem has been posed and solved by that particular analog computer corresponding to a mathematician. However, my deep respect for my mathematician friends requires me not to insist on such an extreme position.

[joking mode off]

Answer 4

While mathematics does not require physics, certain mathematical statements can be understood better with physical examples, the most famous case is maybe the Basel problem how it was explained in 3Blue1Brown:

https://youtu.be/d-o3eB9sfls?si=nLwntZFnDUYH7CGU

Sometimes physics inspires a certain way of proof. I remember seeing a few examples where physics provided a more elegant way of solving a mathematical problem, though it would be hard to find them now. These were some rather artificial problems you find in school olympiads in mathematics.

More often, physics guides mathematics by suggesting problems that are worth studying or directions in which existing models could be extended.

Answer 5

Three fairly recent situations where physics has led to new mathematics:

1. (Homological) mirror symmetry: This goes back to Vafa et al who studied topological string theories. In particular the A-model and the B-model. Without getting to technical, the duality between these models implies that every Calabi-Yau manifold has a mirror manifold, where the Hodge diamond is inverted. Even to assume this at the time would have resulted in the collective shaking of the heads of even the experts in the field. However, physicists insisted and indeed it was later conjectured by Kontsevich that the D-brane categories of both string theories are dual to each other. This is a duality between triangulated $A_\infty$-categories. Namely a certain kind of Fuakaya category and the bounded derived category of coherent sheaves on the complex mirror.

2. 2d-Quantum Gravity and integrable hierarchies: While studying the partition function of two-dimensional gravity, Witten discovered that this function, which is the generating function of the intersection numbers of certain line bundles on the moduli stack of marked Riemann surfaces, could be a tau-function of the so-called KDV-hierarchy that classifies the solitons in a certain integrable model. This was later proved again by Kontsevich using matrix-models. This led to a new area in enumerative geometry which studies the interconnection between integrables hierarchies, spectral covers, conformal field theories, matrix models and two-dimensional gravity. Recent developements are the topological recursion (Kontsevich, Soibelman) and its higher variants connecting four-dimensioal gauge theories to Hurwitz covers and affine-W-algebras.

3. The AGT-correspondence: Somewhat connected to 2. Research is still ongoing. In 2009 physicist found that the instanton partition function of N=2 supersymmetric Yang-Mills theory is a conformal block in two-dimensional higher-spin conformal field theories called affine W-algebras. Losely speaking this is due to the fact that the T-equivariant-cohomology of the instanton moduli space is isomorphic to the Verma-modeules of such affine W-algebras. This has sparked a flood of new developments in mathematics and theoretical physics. Actually, the root for this discovery lies in Seiberg-Witten theory and Nekrasov's work on instanton counting, becuase the u-plane in SW-theory is a spectral cover, which defines an integrable system called a Donagi-Witten system. As stated in 2. such integrable models are deeply connected to affine W-algebras and topological recursion.

Answer 6

A low level example: You use Newtonian mechanics to derive the harmonic oscillator differential equation $\ddot x + kx=0$ from a restoring force $F(x)=-kx$. Of course you can solve this ODE with mathematical tools, but it will require a little bit of time and effort to integrate it.

Using physics you can make a suitable ansatz $x(t)=a\sin(\omega t+\phi_0)$, because you already know that a restoring force will make the body oscillate.

Answer 7

I think that Mathematics can stand alone without Physics as it is subject based only on logic whereas the reverse is not necessarily true.
The basis of Mathematics is a set of rule (axioms) from which logical deductions can be made without any recourse to Physics, then that Mathematics can be applied to Physical problems.
There is a branch of Mathematics called Euclidean Geometry in which parallel lines never meet. Then came Riemannian geometry in which "parallel" lines can meet and initially this branch of Mathematics did not have an application outside of Mathematics until it became useful to describe curved space, etc.
Contrast that to Calculus which was developed to fulfil the needs of the investigation of physical phenomena.
The Mathematics and Physics are intertwined and have contributed to each other throughout history.

Thus your question is really opened ended with some saying that Mathematics is a human construct invented by humans to help develop their knowledge and understanding, some say all that humans can do is discover parts of mathematics which are just "there", and others think it might be a mixture of the two ideas.

Going back to Euclid, he observed and thought about objects and then developed a set of rules (axioms) which became a branch of Mathematics which is useful to Physicist but as to whether Euclidean geometry existed before Euclid, who knows.

Answer 8

Consider the increasing use of electronic computation by mathematicians, both for exploration and for the construction of rigorously formal proofs. While the physics of computation is hidden behind layers of abstraction, those abstractions would be useless without our mastery of electromagnetism and condensed matter physics.

Answer 9

You can take the physics out of mathematics, but you can't take the mathematics out of physics.

Answer 10

It's difficult to fully characterise both fields or all aspects of their relationship, but broadly speaking other fields apply mathematics as a tool for quantification.

It doesn't seem necessary to study physics in order to study mathematics, and mathematics is used in more fields than just physics, so it's not clear that the explicit content of mathematics relies on anything specifically associated with physics - although this is not to exclude the possibility that both rely on something common which is not considered particular to either field.

Indeed, because mathematics is used more generally than just in physics, and if mathematics were seen to be reliant on physics, then it would follow that all other fields using mathematics would become reliant on physics. In such a case, it is likely that academia would respond by redrawing the boundaries between the two fields.

The divisions are only conventional anyway and are ultimately under the control of academics collectively, so unless academia were taken by surprise by the sudden revelation of a hithero unperceived link, then it would not allow the lines to be drawn between academic fields in such a way that most or all other fields depended on something within the scope of physics.

It appears that mathematics is concerned with studying general principles or systems of quantification. In some cases, although the examples escape me now, mathematicians have produced the tools before a scope for their application was known and before there was any specific demand for that tool.

Answer 11

I would like to state some examples to elaborate on the statement that physics can provide intuition to developing strategies to solve mathematical problems:

$\textbf{1. Reflection}$

Consider $2$ points $A$ and $B$ not lying on a particular line(say $l$), and say one has to find a point on line $l$ such that the sum of its distances from $A$ and $B$ is minimum. What point would it be?

To solve this problem, it can be realized that this situation is essentially a consequence of Feynman's principle of least action, which states that

If light has to pass through $2$ points in space, it always takes the quickest path joining them.

Here, it can be applied by considering a light ray emanating from one point that should reach the other point after reflection from the line $l$, hence it will take the path where the distance to be travelled is minimized.

WLOG, let $A$ be a point source of light. Since the angle of incidence is equal to the angle of reflection for the minimum case, if $A$ is reflected about $l$, $2$ congruent triangles$($here, $\Delta ADC\cong\Delta A'DC)$ are obtained:

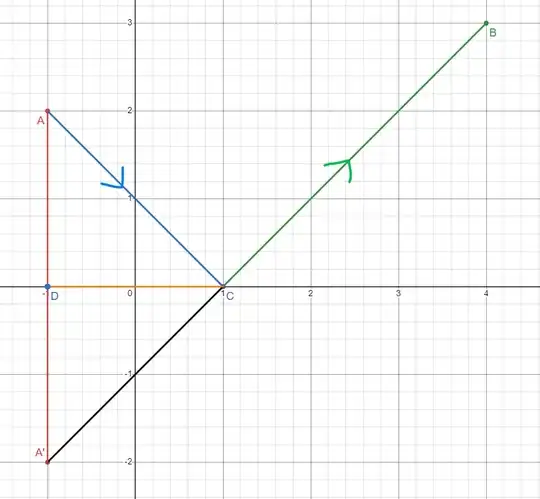(In this picture, I have taken $A\equiv(-1,2), B\equiv(4,3)$ and $l\equiv y=0$)

So, in general, it can be stated that the required point would be the point of intersection of line $l$ and the line joining the image of $A$ or $B$ in $l$ and $B$ or $A$ respectively.

$\textbf{2. Refraction}$

Consider $2$ points $A$ and $B$ on the opposite sides of the boundary between a metalled and an unmetalled road. A car at $A$ has to reach $B$ in the shortest time. What path should it take?

This can also be understood as a consequence of Feynman's principle of least action. Here, we can consider a light ray originating from point $A$ that should reach point $B$ after passing through an interface of $2$ different media, i.e., get refracted. In this case, as the speeds of light in both the media would be different, the quickest path between $A$ and $B$ would be different from the straight line joining them. It would be composed of $2$ straight lines inclined to the normal of the boundary/interface as per Snell's law.

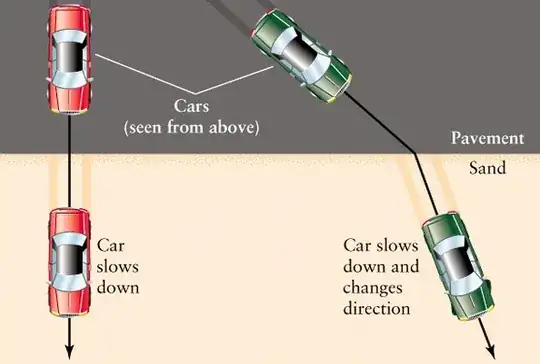
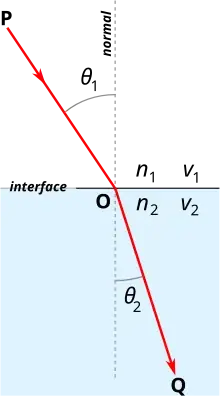
$\textbf{3. Surface Tension}$

Which $2$-D shape has the minimum perimeter for a given area, i.e., encloses the maximum area for a given perimeter?

Or in $3$-D, this can be phrased as:

Which solid has the minimum surface area for a given volume, i.e., encloses the maximum volume for a given surface area?

As the phenomenon of surface tension minimizes the surface area taken up by a given amount of liquid(since potential energy of the surface molecules is minimized in such a case),

• a film of liquid surrounding a $2$-D cavity bounded by a thread would pull it in such a way that the perimeter is least for the given amount of liquid. The circle fits this criterion.
• a droplet of liquid would take such a shape that the surface area is least for the given amount of liquid. The sphere fits this criterion.

Image Courtesy:

$1.$ Reflection

$2.$ Snell's Law in Cars

$3.$ Statement of Snell's Law

$4.$ Soap Film Experiment on Surface Tension

Answer 12

It seems to me that most scientists today more or less adhere to some kind of variant of a physicalist/materialistic worldview.

In this setting, thoughts are the product of the physical configuration of the brain. In particular, to the collection of mathematical thoughts one can have at a given moment must correspond a collection of physical configurations.

Mathematical concepts, then, could be mere mental images (in the sense of functions) of the physical reality of neurons etc. much in the same way than colors happen in our minds whenever a photon of a given wavelength enter our eyes.

In particular, this would imply that the nature of mathematical concepts species could form is strongly dependent on the physical structure of their brain. Although I suspect the brain to be this hyper connected / hyper modulable region of the universe where approximately any structure possible could be realised.

Answer 13

All of mathematics requires physics in subtle and not so subtle ways.

Information is physical: (https://pubs.aip.org/physicstoday/article-abstract/44/5/23/406580/Information-is-PhysicalThere-are-no-unavoidable, https://pubs.aip.org/physicstoday/article/68/9/30/415206/Information-From-Maxwell-s-demon-to-Landauer-s) and, whatever it really is, mathematics certainly involves information.

At the most basic level, geometric proofs require appropriate physical mediums to draw and record steps. Try constructing a right angle with a compass and straight edge on piece of paper, on a sandy beach, or on the ocean. Our ability to find appropriate physical mediums to perform mathematics is perhaps the -1th postulate of mathematics. More generally, proofs require a computer: a processor and memory. Both are physical. What happens when the steps of a proof extend beyond our ability to write them down? What happens if our algorithm needs 100 billion years to solve a problem? You stop doing the problem. Mathematics cannot be performed without suitable physical laws, and is simultaneously being constrained by them.

Answer 14

Absolutely yes.

Math is not a static thing; it grows. More often than not, the results first come as conjectures, supported by physical intuition, and rigorous justification doesn't come for years, sometimes even decades.

Calculus was not rigorously justified for more than a century, from Newton to Cauchy. And during all that time Calculus was used for purely Math purposes.

Probability was not rigorously justified for several centuries, from Pascal to Kolmogorov.

More recently, many path integral related things haven't been rigorously justified yet, 75 year after path integral was introduced by Feynman. And they are being used in Math; for example, Witten's work on knot invariants.

Quantization of mathematical objects obviously grew from Physics. The idea being "In Physics, if you replace the skew-symmetric Poisson bracket with non-commutativity, lots of interesting things come out. So let's look for skew-symmetric operations everywhere we possibly can, in algebra and in geometry, replace that with non-commutativity parametrized by a parameter h, and see what falls out."

Math is not a fossil, preserved in textbooks. Many new things haven't been made rigorous yet, but they are believed because of physical intuition. Of course, a lot of effort goes into making things rigorous. However, more often than not, rigor is the trailing part of the development.

Imagine two mountain climbers, tied together by a rope. The leader is looking for the path forward. The trailing climber does a lot of heavy technical work, hammering in the anchors into the rock. Math is often developed like that. And decades later, in a textbook, you see only the path of anchors, hammered into the slope.

Answer 15

David Hilbert was a famous German mathematician in the early 20C. He discovered the Einstein-Hilbert action from which you can deduce Einstein's field equations for General Relativity.

In 1900 he listed a set of questions whivh he felt would be important for the development of mathematics for the following century. There were 23 questions and the 6th question was about setting out axiomatic foundations for physics.

This is still an ongoing project, especially for QFT. Now I would suggest that the two great mathematical systems inherited by Europe - Euclidean geometry and arithmetic - the former which was axiomatised by Euclid and the latter seen as too basic to be axiomatised until the 20C with Peano's axioms, are both axiomatisations of physical intuition. They were the first two physical theories which were axiomatised. The term 'geometry' hints at that as it merely means measuring the earth. Whereas arithmetic follows from treating individual things as collections. Your headline question asks:

There is mathematics in physics but is there any physics in mathematics?

By the preceding argument we can say that mathematics was born out of physics.

As for a modern example of where physical intuition is indispensible, I would suggest mathematical physics and also physical mathematics.

Answer 16

You have to look at what Edward Witten (the first physicist to receive the Fields Medal)says, Michael Atiyah* said of Witten:

"Although he is definitely a physicist (as his list of publications clearly shows) his command of mathematics is rivaled by few mathematicians, and his ability to interpret physical ideas in mathematical form is quite unique. Time and again he has surprised the mathematical community by a brilliant application of physical insight leading to new and deep mathematical theorems ... He has made a profound impact on contemporary mathematics. In his hands physics is once again providing a rich source of inspiration and insight in mathematics."

Mathematics according to Alain Connes "is a factory that produces ideas".

Being a 'math engineer' means having the ability to invent the new mathematical tools you need to simplify work effectively.

(*) Atiyah–Singer index theorem (he has a link with Dirac's operator)

Answer 17

If you observe, mathematics is all about logic and analytical thinking. It is an abstract subject, as it don't have any physical evidence, although it has a lot of applications and it is quite useful in real world.

When you apply mathematics to the real world, it becomes physics, i.e. applied mathematics is physics.

But the converse is not correct.

Answer 18

The natural laws which make up the universe is physics and contain no mathematics,however if we want to model the universe then we need mathematics to describe the physics.In that case physics is no different than biology,there are models in biology which need mathematics otherwise they become too vague.

Mathematics is a tool to make a branch of science less vague for a human.

Answer 19

Answer from a mathematician (graduate student). I think many answers and the question itself don’t take into account that pure mathematics as a research area is full of physics. There is the quite huge field of pure mathematics that studies Partial Differential Equations. People take equations (mostly) from physics, and try to study them from a purely analytical point of view.

— (easy example: you can consider the ODE $\ddot x=-C/|x|^2$ coming from planet-star systems, and prove with absolute mathematical rigor all 3 of Kepler’s laws for the solutions $x(t)$ of the ODE) —

It’s a situation where the models being studied come from physics but they are considered as mathematical models, the problems themselves are purely mathematical (in the sense that they are mathematical statements, independent of the physical reality), and the techniques used are of course purely mathematical, but physics knowledge and understanding is often incredibly helpful, if not absolutely necessary.

One example. The existence of conserved (or monotone) quantities adapted to specific PDEs (like mass, energy, entropy,…) is incredibly useful mathematically to prove essentially anything. Without any physical intuition at all, it would be difficult to imagine there exists some mathematical quantity that has the characteristics of entropy, let alone finding it or thinking of using it.

You might say that we PDE people are just basically doing physics, but then (besides feeling absolutely unworthy of such a honor) I could reply that half of pure mathematics comes from physics anyway, one way or another… X) And I would say that often we don’t even study PDEs that come directly from physics (for instance, we might consider toy models to test some mathematical techniques), but physical intuition still helps. So my answer would be “in practice, yes”.

Answer 20

I'd think a new branch of logic is a mathematical problem inspired by physics.

https://en.wikipedia.org/wiki/Quantum_logic

"In the mathematical study of logic and the physical analysis of quantum foundations, quantum logic is a set of rules for manip­ulation of propositions inspired by the structure of quantum theory."