I am following Variational Principles of Mechanics by Lanczos, 4th edition, 1970 on the page 360 forward.
He is deriving the Euler equations of fluid flow.
He starts by defining the kinetic and potential energies to come up with a Lagrangian:
$$T=\rho \frac{v^2 }{2}dV$$
$$U=\rho \varphi dV$$
where $\rho$ is the density of the fluid and $\varphi$ is the Newtonian potential of gravity.
The action is:
$${\displaystyle {\mathcal {S}}=\int _{t_{1}}^{t_{2}}\int_V \mathcal L\,dVdt}=\int _{t_{1}}^{t_{2}}\int_V\rho \left(\frac{v^2 }{2}-\varphi\right)dVdt.$$
He also says that we have to add the condition that the variation of any volume vanishes and that gives rise to a Lagrangian multiplier $p$:
$$\nabla \cdot\delta x=0 \implies \int _{t_{1}}^{t_{2}}\int_V p \nabla \cdot (\delta x) dVdt $$
also, because
$$p \nabla \cdot (\delta x) = \nabla \cdot (p\delta x)-\nabla p \cdot \delta x$$
and because of the Gauss divergence theorem the first term vanishes.
Our action integral becomes
$${\displaystyle {\mathcal {S}}}=\int _{t_{1}}^{t_{2}}\int_V[\rho \left(\frac{v^2 }{2}-\varphi\right)-\nabla p \cdot \delta x] dVdt.\tag1$$
He also says that the variation is restricted by the condition that the mass should not be varied:
$$\delta (\rho dV)=0$$
He obtains
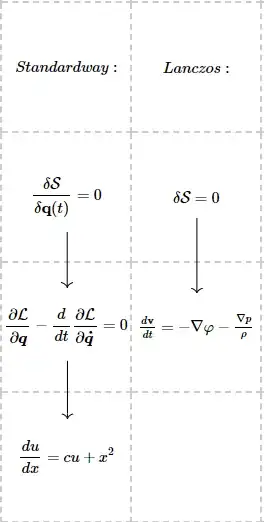
$$\frac{d \mathbf v}{dt}=-\nabla \varphi -\frac{\nabla p}{\rho}$$
which are the Euler equations in the Lagrangian picture.
We can change the picture to Eulerian and obtain the standard form
$$\frac{d \mathbf v}{dt}+\mathbf v \nabla \cdot \mathbf v=-\nabla \varphi -\frac{\nabla p}{\rho}.$$
My question:
1. He doesn't actually show the steps of the variation. Does someone know how to approach this variation? I don't know through what to vary this. Usually we do the path variation.
2. Can we use the definition of the Lagrangian that is written in the equation $(1)$ i.e.:
$$\mathcal L=\rho \left(\frac{v^2 }{2}-\varphi\right)-\nabla p \cdot \delta x$$
and input it in the standard Euler-Lagrange equations:
$${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial {\boldsymbol {q}}}}-{\frac {d}{dt}}{\frac {\partial {\mathcal {L}}}{\partial {\boldsymbol {\dot {q}}}}}=0}$$
and still obtain the equations of motion, i.e. the Euler equations?
In general, through variation of the action integral we obtain the Euler-Lagrange equations which we than have to solve to obtain the differential equations governing the dynamics of the system.
In this derivation, on the other hand, it seems that he does the variation and immediately obtains the equations governing the dynamics of the system, i.e. the Euler equations.
Am I misinterpreting something or are the Euler equations actually Euler-Lagrange equations for fluid flow?