-3

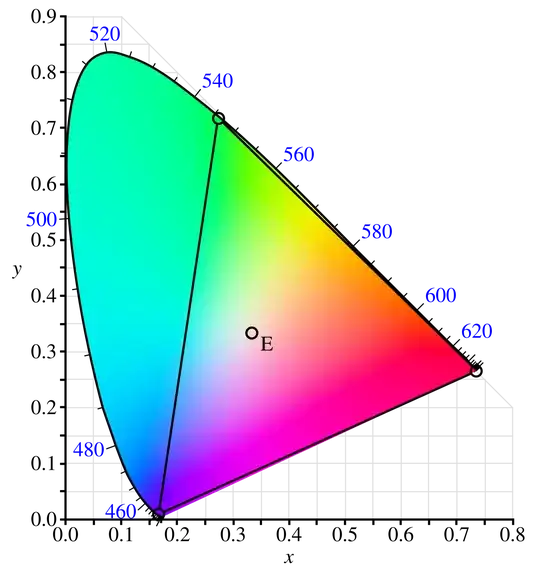
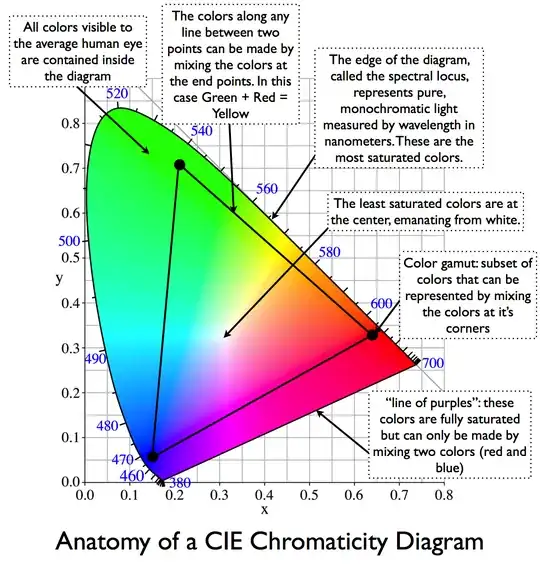
Is it true that we can only see colors that lie in the visible spectrum? If yes, then why can colors like RGB $(168, 151, 80)$ be seen by humans?

Let us suppose that we are at the extremely red part of the visible light spectrum; then, the RGB value will be $(255, 0, 0)$. If we start going to the right-side of it, then the value of the red component starts to decrease, and the value of the green component starts to increase, but since we have not crossed the green part yet, the value of the blue component will be zero. Once we reach the green part, the RGB value will be $(0, 255, 0)$. Now, when we go further to the right, then the value of the green component will start to decrease, and the blue component will start to increase. So, at any given time, at least the RGB values will be zero.

So, colors like RGB $(168, 151, 80)$, in which all 3 components are nonzero, do not lie within the visible light spectrum and cannot be seen.

Visible Spectrum

Here is the photo of the visible spectrum that I am referring to.

Vincent Thacker
  • 15,416
Anshul Gupta
  • 111

2 Answers2

5

The colors we can see are described by a 3 dimensional color space. There are many ways to define coordinates for such a space. RGB is one of them. In these coordinates we can see any color where each coordinate is between $0$ and $255$.

We can even see beyond these values. This color space describes the colors a computer monitor can display. We can see redder reds, bluer blues, and greener greens than a monitor can display.

The CIE color space is more suitable for describing vision. The CIE chromaticity diagram is a common way to display a $2$ dimensional slice of this space. This slice is at constant saturation. E.G. It shows red, but not pink or dark red.

Monochromatic colors are the curved boundary line. These are the colors of the rainbow, the reddest red and so on.

The colors you can form by mixing three colors forms a triangle in this space. The triangle drawn uses the reddest red, greenest green, and bluest blue.

The triangle of RGB colors with vertices $(255,0,0)$, $(0,255,0)$, and $(0,0,255)$ is also inside the colored region. The color you get when you tell your computer to display an RGB color depends on your particular monitor. The bottom diagram is an example. This is from the Sharp Color Science Tool page

CIE 1931 Chromaticity diagram

Chromaticity diagram with RGB colors

mmesser314
  • 49,702
2

RGB is a spectrum computers use to display colour. It doesn't bound the colours we're able to see, it is bound by the colours we're able to see (because why would computers display colours we can't see?), but even assuming it did, I still don't see why RGB wouldn't be "valid" to you if we imagine it as a graph with 3 axes. Your issue is trying to bound it to 2.

Paolo Mancini
  • 61