Intuitive access to stress, pressure, shear at a point as compared to a singe force vector at this point

Question

Wikipedia writes

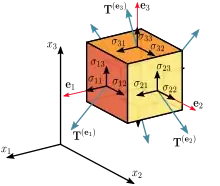
stress is also a fundamental quantity

But why fundamental? Let me try to explain my confusion: the Cauchy Stress Tensor (image from Wikipedia)

provides three vectors (the tensor) for a point with 6 degrees of freedom. One "force per area" vector per the (linearly independent) planes meeting in the point.

On the other hand: don't we have a single effective force vector on that point? And if we know this force, which information is missing compared to the stress tensor?

An explanation appealing to intuition would be great, though I know intuition can be quite individual. I imagine sitting in this point and feel being pushed and shoved by my surrounding points and I know these are all forces. But I also know that at a specific instance in time, the forces add up to just one resulting force vector. Why take account of the three planes and respective force vectors acting on them?

Edit: I start to wonder whether my intuition of "force on a point" is nonsensical. If I push a button, I cannot ask for the force on an infinitesimally small point of the button. It is infinitesimally small, "zero" so to say. Without integration over an area there is nothing. And so we have the force per area coming in naturally. Hmm, I wasn't aware force is so finicky.:-)

Answer 1

Stress in balance equation

I agree with your edit that the intuition of a "force on a point" is not a correct premise to start with.

don't we have a single effective force vector on that point?

Indeed in the continuum representation of bodies, there is no single effective force on a given point but rather densities of external forces that are balanced by the stress field's divergence. This is what the local static balance suggests:

$$ \mathrm{div}\,\boldsymbol\sigma + \rho\boldsymbol f = \boldsymbol0. $$

So the only way (I can find) to think of such local forces is as this density of external forces $\rho\boldsymbol f$ expressed in $N/m^3$. Here the divergence is what becomes of the bounding surface integral of a volume that shrinks to infinitesimal size.

But there are other ways to interpret the stress tensor.

Stress as a vector-valued operator

Why take account of the three planes and respective force vectors acting on them?

It is more than three planes: the stress tensor provides information on any infinitesimal oriented surface.

In that sense it is useful to think of the stress as a linear operator. To any location $\boldsymbol x$ and unit direction $\boldsymbol n$ the stress can associate the traction vector

$$ \boldsymbol t=\boldsymbol\sigma\boldsymbol n $$

There are an infinity of directions at each point and the stress tensor contains all the necessary information to describe the surface forces acting upon them.

Stress as a scalar-valued function

Finally another fruitful view of the stress tensor is as a bi-linear form. Indeed the power of internal forces reads

$$ p_\mathrm{int} = \boldsymbol\sigma:\dot{\boldsymbol\varepsilon} $$

which represents the mechanical volume energy per unit time that the material exchanges with external sources. Here $\dot{\mathbf\varepsilon}$ is the strain rate which describes the local deformation. So from that perspective the stress tensor can be seen as a (multi-linear) function that returns the power of internal forces given the body's deformation*.

As a matter of fact this is exactly how it is introduced in modern variational approaches to continuum mechanics (e.g. Salencon's handbook, p.191): as part of a pragmatic way to model the power of internal forces as a function of the velocity field and it's gradients .

Answer 2

In general, there's no reason why the normal forces and tractions on any given infinitesimal element shouldn't produce a net force and a net moment on that element, which I think includes the "single effective force" that you're describing.

However, elasticity—the study of stresses and strains—typically addresses the stress state and deformation once the bulk motion has been removed; thus, the stress tensor is constructed to leave no residual force or torque on an infinitesimal element, such that there’s no translational or rotational acceleration of that element. Those accelerations are generally treated in a separate field: dynamics.

An example is the pure shear state, where fully four traction forces are required for static equilibrium, because a lack of any one of them would produce bulk motion:

(Images from my site, a page in progress.)

Answer 3

The Cauchy stress relationship allows you to determine the traction vector on a plane of arbitrary orientation, given the stress tensor and the unit normal to the plane. The traction vector is the force per unit area of the material on the side of the plane towards which the normal is directed on the material on the side of the plane from which the normal is directed. The traction vector is equal to the stress tensor dotted (contracted) with the normal.