5

I have read this question:

For light elements, roughly up to iron ($\mathrm{Fe}$), splitting atoms actually costs energy, rather than energy being released.

How much energy is released from the splitting of a single hydrogen atom?

Question:

  1. Why is it that for light elements, roughly up to iron ($\mathrm{Fe}$), splitting atoms actually costs energy, rather than energy being released?
M. A.
  • 2,039
  • 5
  • 11
  • 28
Árpád Szendrei
  • 30,008

1 Answers1

5

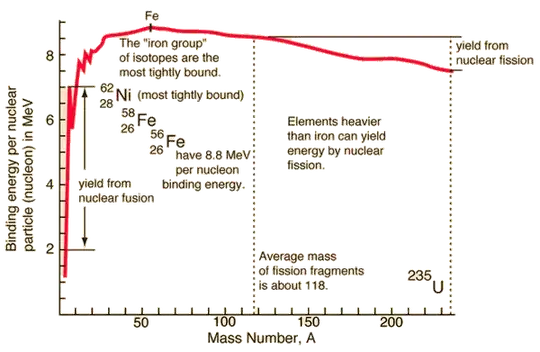
The relationship between the energy required to split the nucleus (the "binding energy") per nucleon and the mass number forms a characteristic curve for the elements.

For light elements (up to iron), as nucleons are added, the binding energy per nucleon increases, reflecting the dominance of the strong nuclear force over the Coulomb repulsion. Thus, fusing light elements (like hydrogen and helium) releases energy, while splitting them costs energy. As you approach iron (mass number $\approx 56$), the binding energy per nucleon reaches its maximum (resulting in a very stable nucleus). Beyond iron, adding more nucleons leads to a net decrease in the binding energy per nucleon. Consequently, splitting these heavier nuclei releases energy due to the formation of more stable products with higher binding energies per nucleon.

Here's a plot of the binding energy per nucleon as a function of the mass number I borrowed from HyperPhysics.

enter image description here

IntegerEuler
  • 219
  • 6