Derivation of the Fresnel equations and the fact that the incident, reflected, and transmitted waves are coplanar

Question

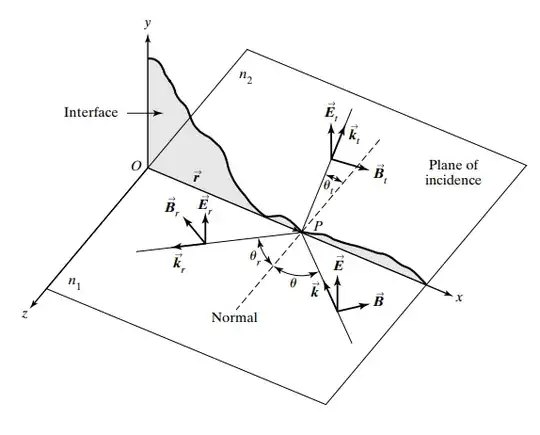
I am self-studying Optics by Pedrotti. In Chapter 24 of the 3rd edition, Pedrotti derives the Fresnel Equations accompanied by the figure below. I don't understand Pedrotti's proof that the incident, reflected, and transmitted waves are coplanar. I have seen this answer which provides a more involved justification of why they must be coplanar, but I am curious about Pedrotti's simple justification.

I'll state my question here and then provide background below.

How is it that the conditions

$$ (\vec{k} - \vec{k}_r) \cdot \vec{r} = (\vec{k} - \vec{k}_t) \cdot \vec{r} = (\vec{k}_r - \vec{k}_t) \cdot \vec{r} = 0 $$

imply that $\vec{k},\vec{k}_t,\vec{k}_r$ are coplanar?

For example, $(\vec{k}-\vec{k}_t)\cdot\vec{r} = 0$ implies that $\vec{k}-\vec{k}_t$ is perpendicular to $\vec{r}$, but not necessarily that it lies in the plane of $\vec{k}$ and $\vec{r}$. Why couldn't $\vec{k}_t$ have a component that is out of the plane of incidence?

Pedrotti writes:

In the boundary plane $xy$, where all three waves exit simultaneously, there must be a fixed relationship between the three wave amplitudes (and thus their irradiances) that has yet to be determined. Since such a relationship cannot depend on the arbitrary choice of a boundary point $\vec{r}$ nor a time $t$, it follows that the phases of the three waves, which depend on $\vec{r}$ and $t$, must themselves be equal: $$ (\vec{k} \cdot \vec{r} - \omega t) = (\vec{k}_r \cdot \vec{r} - \omega_r t) = (\vec{k}_t \cdot \vec{r} - \omega_t t) $$ In particular, at the boundary point $\vec{r} = 0$ of Figure 1, $$ -\omega t = -\omega_r t = -\omega_t t $$ or $$ \omega = \omega_r = \omega_t $$ so that all frequencies are equal. On the other hand, when $t=0$, $$ \vec{k} \cdot \vec{r} = \vec{k}_r \cdot \vec{r} = \vec{k}_t \cdot \vec{r} $$ Several conclusions can be drawn from this equation. First notice that by subtracting any two members, these relations are equivalent to: $$ (\vec{k} - \vec{k}_r) \cdot \vec{r} = (\vec{k} - \vec{k}_t) \cdot \vec{r} = (\vec{k}_r - \vec{k}_t) \cdot \vec{r} = 0 $$ which requires that the vectors $\vec{k}$, $\vec{k}_r$, and $\vec{k}_t$ lie in the plane determined by the vectors $\vec{k}$ and $\vec{r}$. Thus all three propagation vectors are coplanar in the $xz$-plane, and we conclude that the reflected and refracted waves lie in the plane of incidence.

Answer 1

Explicitly, in terms of the components, we have: $$\begin{align*} \mathbf{k}\cdot\mathbf{r}=\mathbf{k}_r&\cdot\mathbf{r}=\mathbf{k}_t\cdot\mathbf{r},~~~\mathrm{for}~z=0\\ \implies xk_x+yk_y&=xk_{rx}+yk_{ry}=xk_{tx}+yk_{ty} \end{align*}$$ This requires the components to be equal separately:

$$\begin{align*} k_x&=k_{rx}=k_{tx}\\ k_y&=k_{ry}=k_{ty} \end{align*}$$

Of course, to make it even easier to see, we are free to orient our coordinate system such that the incident wavevector lies in the $xz$-plane, which amounts to the component $k_y=0$. But we know that the reflected and transmitted wavevectors must have the same component, so they must also lie in the same plane.

Alternatively, we can use the expressions $$\begin{align*}(\mathbf{k}-\mathbf{k}_r)\cdot\mathbf{r}&=0\\(\mathbf{k}-\mathbf{k}_t)\cdot\mathbf{r}&=0\end{align*}$$ to see that the difference vectors $(\mathbf{k}-\mathbf{k}_r)$ and $(\mathbf{k}-\mathbf{k}_t)$ must be perpendicular to $\mathbf{r}$. Also see that the tangential components of the wavevector must be continuous across the boundary (which is equivalent to the above equality of components statement). These two facts taken together can only be true if the difference vectors are some multiples of the boundary normal vector $\mathbf{n}$. Because of this, we can write: $$\begin{align*}\mathbf{k}-\mathbf{k}_r&=a\mathbf{n}\\\mathbf{k}-\mathbf{k}_t&=b\mathbf{n}\\\implies\mathbf{k}-\mathbf{k}_r&=\lambda(\mathbf{k}-\mathbf{k}_t)\\\implies\alpha\mathbf{k}+\beta\mathbf{k}_r+\gamma\mathbf{k}_t&=0\end{align*}$$ This establishes the vectors as linearly dependent, and as such they must be coplanar.