How does time dilation appear from two different frames of reference?

Question

I am reading a modern physics book out of general interest. The special relativity chapter uses a fixed observer as $O$ and an observer on a train as the moving reference frame $O'$ to explain time dilation. I understand the logic behind $O$ measuring a longer time interval than $O'$. Effectively this means that $O$ ages faster than $O'$. Where I get confused is considering the situation from $O'$. $O'$ looking back would see $O$ in motion with respect to him. Which means that $O'$ measures a longer time interval and ages more than $O$, but this seems like a contradiction. You can make a similar case for length contraction. Is this the correct way to understand the situation and if not how is it resolved?

Answer 1

You have it right. $O$ sees $O'$ aging more slowly and himself aging normally, while $O'$ sees $O$ aging more slowly and himself aging normally.

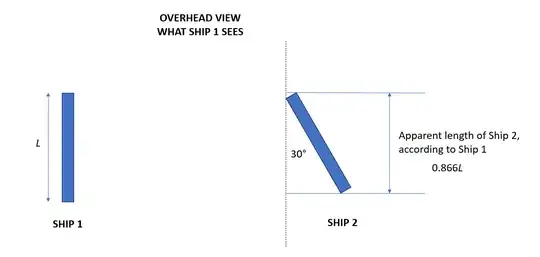
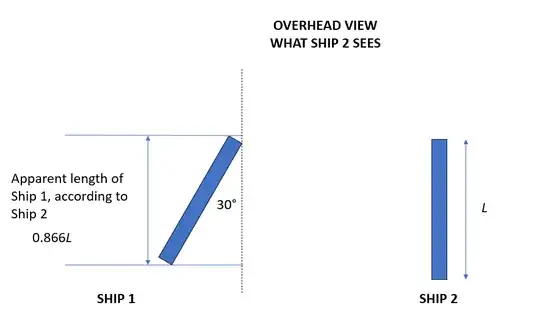
Let us say we have two ships meet in the ocean. Each ship is identical, and each is 100 m long. The ships are rotated 30° to each other, however, and each can only measure the length of the other visually. What will each one measure? As you can see in the figures below, by measuring the normal projection of the opposite ship that faces it, the crew of Ship 1 will measure Ship 2's visual length to be 86.6 m, while measuring their ship's own length to be the expected 100 m. The crew of Ship 2 will measure exactly the same thing from their point of view - Ship 1 will appear to be 86.6 m in their scope, and their own ship will appear to be 100 m. Both points of view are exactly symmetrical, and there is no sense in asking which of them is "correct." The only meaningful thing you can say is that the ships are rotated 30° to each other.

Now Lorentz transformations or "boosts" are rotations in spacetime, rather than just in space. If two objects are moving at relative speed $v$, each one will measure a projection of the other's space intervals and time intervals, and thus (for example) the $O$ observer will see that the time-separation of events in the $O'$ ship are slowed compared to the same events seen from within the $O'$ ship. And vise versa. Again, you cannot say who is "correct." You can only meaningfully say that $O$ and $O'$ are moving at a relative speed of $v$.