The development of Clausius Inequality

Question

The reversible cyclic device absorbs $\delta Q_R$ from the thermal reservoir at $T_R$ and rejects heat $\delta Q$ to the piston-cylinder device, whose temperature at that part of the boundary is $T$ (a variable), while producing work $\delta W_{rev}$. The system produces work $\delta W_{sys}$ as a result of this heat transfer.

Applying the first law of thermodynamics yields

$ \delta Q_{R} - dE_{C}=\delta W_{C} $

Where $\delta W_C$ is the total work produced by the system. Why does the book consider the cyclic device as reversible when we are rejecting heat to the piston cylinder (system), which is not a thermal reservoir since its temperature is varying? Shouldn't heat transfer through a finite temperature difference cause the process to be irreversible?.

The book then says that if we let the system undergo a cycle while the cyclic device undergoes an integral number of cycles. Then it appears that the combined system is exchanging heat with a single thermal reservoir while producing work during a cycle. On the basis of the Kelvin-Planck statement, $W_C$ cannot be a work output, and thus it cannot be a positive quantity.

$ W_{C}= \oint T_{R} \frac{\delta Q_{R}}{T} $

Considering that $T_R$ is the thermodynamic temperature and thus is a positive quantity, we must have

$ W_{C}= \oint T_{R} \frac{\delta Q_{R}}{T} \leq 0 $

To continuously reject heat to the system, the systems temperature must always be less than or equal to the temperature of the cyclic device during the heat rejection process. If we follow the book's assumption that all of the heat rejected by the cyclic device to the system is converted to work during (isothermal expansion I think), then the internal energy of the system will not change. If we let the system undergo a cycle, we recover the work produced by the system from the surroundings and convert it to heat for the cyclic heat engine. How can heat be transferred from the cyclic device to the system and from the system to the cyclic device?

Also if the Kelvin Planck Statement applies to heat engines and the combined system operates on a cycle (the combines system is not a heat engine; yes it receives heat from a high-temperature source and converts part of this heat to work, but it doesn't reject the remaining waste heat to a low-temperature sink. If we perform an energy balance on the combined system, it will not satisfy the first law of thermodynamics because the work produced by the system during the first part of the cycle will cancel the work done by the surroundings. The forms of energy left are the heat received by the cyclic device and the work produced by the cyclic device as it undergoes an integral number of cycles.

The book I am referring to is Thermodynamics: Thermodynamics: An Engineering Approach by Michael A. Boles and Yunus A Çengel (9th edition)

Answer 1

The idea is that you consider any sequence of states for the system, including even out-of-equilibrium states, but such that it finishes back in the state it started in. You arrange that the heat transfer to and from the system takes places via some part of it which is large enough to allow the transfer but can be small compared to the whole system. In this way the part where heat transfer takes place can be assigned a temperature $T$. Note, I have not mentioned the reversible cyclic device yet.

Now we argue that whatever heat is going into the system, or coming out of the system, during each change of state, there is always a reversible cyclic device that can deliver or receive exactly that amount of heat while completing a cycle. You see the reversible cyclic device (e.g. a Carnot cycle) can be arranged to have whatever temperature is required. So heat transfer to and from the system can be accomplished, and we can apply the equation $$ \frac{dQ_R}{dQ} = \frac{T_R}{T} $$ which describes the Carnot engine.

The rest of the argument involves first arguing from Kelvin statement that $$ \oint dQ_R \le 0 $$ from which it follows that $$ \oint \frac{dQ}{T} \le 0 $$ (since we have $T_R > 0$).

Answer 2

The situation in the Cengel-Boles book is as follows. The reversible cyclic engine is operating as a Carnot cycle, its operating temperature at the high end is fixed, $T_R$, where it absorbs entropy in the amount of $S_R=\frac{\delta Q_R}{T_R}$. At the low end its temperature, $T$, may vary with whatever the temperature of the expanding or compressing cylinder has but no matter what, here it is assumed that the cycle of this Carnot engine is reversible*.

Consequently, at the lower temperature, it will reject an amount of $S_R=\frac{\delta Q}{T}$ into the cylinder that is at that temperature $T$ or rather its temperature is an infinitesimally lower than that of the Carnot engine to facilitate reversible heat conduction between them. How this transfer is mechanized is another question but the assumption itself underlies the thinking in the book. The reversible engine executes a Carnot cycle, so that between the isothermal thermal energy exchanges at $T_R$ and $T$ there are two reversible adiabatic stages during which the Carnot engine's entropy does not change. Its entropy at the higher isothermal stage would increase by $S_R$ followed by an adiabatic stage during which its entropy is constant, then an isothermal stage at $T$ the C engine dumps that $S_R$ into the cylinder the end of which the C engine's entropy is the same as it was at the start of the isothermal stage at $T_R$, and when it raises its temperature back to $T_R$ from $T$ via an adiabatic stage, it will have completed its reversible cycle and is back to its original state.

Depending on whether the cylinder is compressing or expanding its temperature changes independently of what the Carnot engine does. They are thermally coupled only when the Carnot engine is at the same or infinitesimally close temperature as the cylinder has to allow the entropy $S_R$ from the Carnot engine to the cylinder flow reversibly. There is no continuous rejection of heat in to the "system" (cylinder). When the C engine and cylinder have different temperatures they are not coupled, e.g., when uncoupled during the adiabatic stages of the C engine, the cylinder expands adiabatically, work is extracted form it and cools to a lower temperature. To effect a lower temperature entropy absorption, in its next cycle the C engine is allowed also to cool at a lower temperature during its adiabatic work stage.

Answer 3

Now that you have given us the name of "the book" discussed in your post I have obtained a copy and had the opportunity to review the relevant material (Chapter 7, Sec 1). Seeing the full context of the material, for the benefit of others who have not read the authors's analysis, I will summarize my understanding of it below which includes equations not provided in your post.

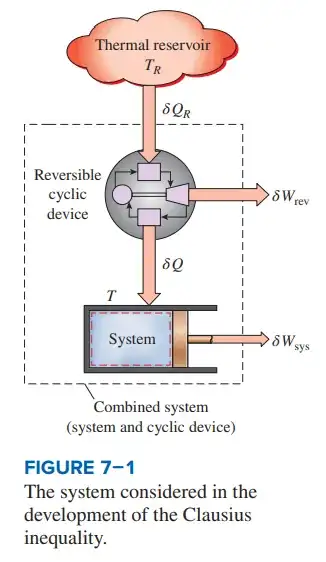
1. Referring to FIGURE 7-1, the authors apply the first law to the “combined system” obtaining

$$\delta W_{C}=\delta Q_{R}-dE_{C}\tag{1}$$

Where $dE_{C}$ and is a differential change in internal energy of the combined system and

$$\delta W_{C}=\delta W_{rev}+\delta W_{sys}\tag{2}$$

2. The authors state that considering that the cyclic device is a reversible one, the following relationship applies

$$\frac{\delta Q_{R}}{T_{R}}=\frac{Q}{T}\tag{3}$$

Where $T$ is the temperature at the boundary between the reversible cyclic device and piston/cylinder system. Note this is equivalent to a single Carnot cycle operating between temperatures $T_R$ and $T$ (more on this below).

3. The authors combine equations (1) and (3) to obtain

$$\delta W_{C}=T_{R}\frac{\delta Q}{T}-dE_C\tag{4}$$

4. The authors then ask us to consider the situation where the system (piston/cylinder device) undergoes a cycle while the reversible cyclic device undergoes an integral number of cycles. Under these conditions, since both devices return to their original states there would be no change in internal energy (as state function) for the combined system, i.e., $dE=0$. Thus equation (4) becomes

$$\delta W_{C}=T_{R}\frac{\delta Q}{T}\tag{5}$$

Then integrating for the combined system gives

$$W_{C}=T_{R}\oint\frac{\delta Q}{T}\tag{6}$$

5. Finally, the authors point out that since the Kelvin-Planck statement of the second law prohibits a system from producing a net amount of postive work while operating in a cycle and exchanging heat with a single thermal reservoir (in this case, $T_R$), it follows that $W_{C}$ cannot be a positive quantity. Or, given $T_R$ is a positive quantity, they state

$$\oint\frac{\delta Q}{T}\le 0\tag{7}$$

Which is the Clausius inequality, with the equal sign applicable if both devices in the combined system are reversible.

YOUR QUESTIONS/COMMENTS:

Given the above, the following is in response to your specific questions and comments on the authors' analysis.

Applying the first law of thermodynamics yields

$$ \delta Q_{R} - dE_{C}=\delta W_{C}$$

Where $\delta W_{C}$ is the total work produced by the system.

Presumably, you meant "the combined system" as the authors stated, and not the "system" which they label as the piston/cylinder component of the combined system.

Why does the book consider the cyclic device as reversible when we are rejecting heat to the piston cylinder (system), which is not a thermal reservoir since its temperature is varying?

There is no requirement that a reversible cycle can only exchange heat with fixed thermal reservoirs. The temperatures of the heat source and sink can vary, as long as they vary in such a way that the difference in temperature between the cyclic device and the heat sink/source continues to be infinitesimal. Under such conditions heat is reversible.

An example is the reversible otto cycle where temperature of the heat sink and source varies during the reversible constant volume heat addition and heat rejection processes.

To continuously reject heat to the system, the systems temperature must always be less than or equal to the temperature of the cyclic device during the heat rejection process.

If the cyclic device is operating as a reversible heat engine, then the temperature $T$ in Fig 7-1 must always be infinitesimally less than or equal to the temperature at which heat is rejected from the cyclic device. But if the cyclic device is operating as a reversible refrigerator/heat pump, the temperature $T$ need only be infinitesimally greater than the temperature at the input of the cyclic device.

If we follow the book's assumption that all of the heat rejected by the cyclic device to the system is converted to work during (isothermal expansion I think), then the internal energy of the system will not change.

To be clear, as stated in my point 4 above, the book's assumption is the internal energy (a state property) of the combined system will not change if the the system undergoes a cycle (returning its properties to their original state) and the reversible cyclic device undergoes an integral number of cycles (returning its properties to their original state).

If we let the system undergo a cycle, we recover the work produced by the system from the surroundings and convert it to heat for the cyclic heat engine. How can heat be transferred from the cyclic device to the system and from the system to the cyclic device?

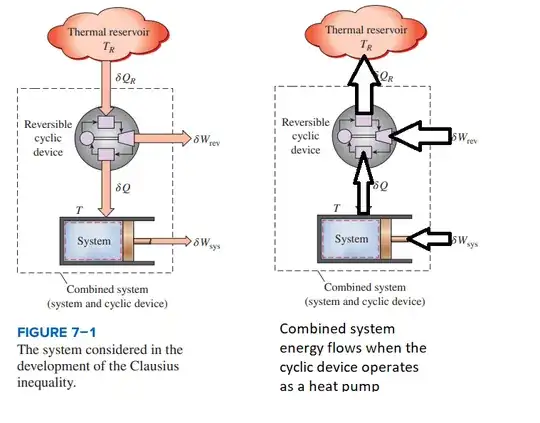
Heat can be transferred from the system to the cyclic device as an input to the cyclic device if the cyclic device is now operated as a refrigerator or heat pump. The system temperature $T$ is infinitesimally greater than the temperature at the input to the cyclic device, resulting in the cyclic device operating as a refrigerator/heat pump as a discussed above. The cyclic device then rejects heat $Q_R$ to the thermal reservoir $T_R$.

But to do so there is now required to be a net positive input work, $W_C$, originating from outside the combined system so that the Clausius statement of the second law is not violated, which is: No refrigeration or heat pump cycle can operate without a net work input. Then, for energy conservation, $\delta Q_{R}= \delta Q + \delta W_C$

I'm unable to understand the final paragraph of your post to be able to comment at this time. Given the above, perhaps you can clarify it further.

Hope this helps.