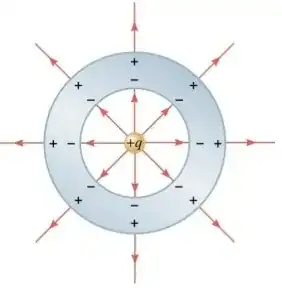
What I mean by my question is: the $+q$ charge that is induced at the outer surface, why does it only induce an electric field outside the sphere? Why is there no field also inside the sphere that terminates at the $-q$ charges that's on the inner surface? I'm not asking about the electric field inside the cavity.
2 Answers
Why is there no Electric field inside a Spherical conductor with Spherical Cavity?
Conductors obey Ohm's Law. The microscopic version of Ohm's Law states that
$\vec{J}=\sigma\vec{E}$
where $\vec{J}$ is current density, and $\sigma$ is the conductivity of the conductor.
In an electrostatic situation, there are no currents. Therefore,
$\vec{J} = 0 = \sigma\vec{E}$
Since $\sigma$ is never $0$ in a conductor (or it wouldn't be a conductor), it must be the case that
$\vec{E}=0$
Thus, there is NEVER an electric field inside a conductor in the electrostatic case. The shape of the conductor does not matter. Nor does it matter whether there is charge "enclosed" by the conductor. Nor does any other factor matter. The fact that there is no current, and Ohm's law is obeyed, is all that matters. This is a good fact to remember.
- 3,825
the charge $+Q$ will lower the potentials of the charge $-Q'$ on the inside of the hollow sphere and would lower it by a significant amount such that $-Q$ charge leaks into the cavity neutralizing the charge there and redistributing the charge on both the inside and the outside surface. THIS could help on understanding how the charges reside on the surface and how they leak into the medium, assuming vacuum in this case however any other dielectric medium would have similar effects but instead of charge leaking in it would just transmit charge(by transmit i mean development of opposite charges).
- 400
- 2
- 15