-1

I hope this is the right place for this kind of post.

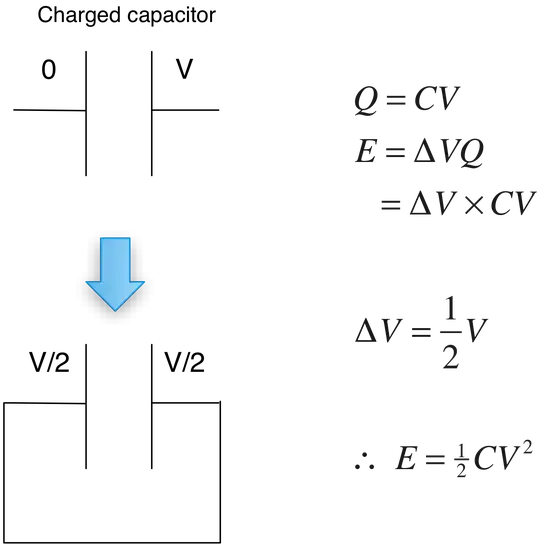
A friend is trying to derive the equation for the energy stored in a capacitor by analysing the change in potential on one plate when the capacitor is shorted, however I don't think this valid. Could anyone explain why this is right or wrong?

He says that when the capacitor is shorted the potential at each plate changes by V/2 (from 0 to V/2 on one side and from V to V/2 on the other), so by substituting in V/2 into the equation he gets E = 1/2 QV, the capacitor energy equation.

Diagram

Qmechanic
  • 220,844
alexdavey
  • 210

2 Answers2

1

Your friend's analysis is flawed for an obvious reason as well as a subtle reason.

First, an obvious flaw is labelling each plate with a voltage. How is this to be interpreted? For example, with respect to what does the right hand plate have voltage $V$?

In essence, your friend is treating each plate as a capacitor in its own right with an associated voltage and thus stored energy. That's OK as long as it is acknowledged as such. For example:

enter image description here

Clearly, in the above, we can define a voltage on either conductor, relative to the reference conductor (ground) as well as a voltage across.

But, crucially, there are 3 capacitors and associated capacitance, voltage, and stored energy to consider.

And this leads to the subtle flaw which is related to the two capacitor missing energy paradox.

I'll leave that as an exercise for your friend.

Community
  • 1
Alfred Centauri
  • 60,633
0

The factor of $1/2$ comes because you integrate need to integrate:

$$ E=\int_0^V C V dV = \frac{1}{2} C V^2 $$

Dave
  • 4,203