Minkowski's interpretation of Increase of relativistic mass for moving object

Question

Minkowski's spacetime gives an easy interpretation of space and time contraction as the projection of space and time for the (hyperbolic) rotated reference frame of the moving object on the observer's frame of reference. Is there a similar insight in Minkowski spacetime for the increase in relativistic mass of the moving object? I follow that the total energy of the moving object is higher than its rest energy and relativistic mass is proportional to total energy, but I'm looking for a more geometrical visualization. Perhaps something like the total energy of the rest frame is now contained in a smaller total spacetime volume, so energy density increases? Could be chasing up the wrong tree here but would appreciate any clarification.

Answer 1

Is there a similar insight in Minkowski spacetime for the increase in mass of the moving object?

In the usual Minkowski formulation mass does not increase, it is a relativistic invariant.

The invariant mass is calculated as the Minkowski “length” of the four-momentum: $$m^2 c^2=E^2/c^2-p^2$$ This formula recovers Einstein’s famous $E=mc^2$ for $p=0$ and the photon’s $E=cp$ for $m=0$.

I follow that the total energy of the moving object is higher than its rest mass and mass is proportional to total energy

In the usual formulation mass is equal to the center of momentum frame energy, not total energy. The total energy is the frame-variant time component of the four-momentum. The mass is the Minkowski norm of the four-momentum.

Relativistic mass is just another name for total energy. Since we already have the term total energy, having a second name is redundant. The Minkowski norm is a separate quantity, so it is useful to have a name for it. So we use mass to refer to the invariant norm rather than as a duplicate of total energy.

Answer 2

No.

The natural objects in Minkowski space are Lorentz scalars, 4-vectors, etc, and there is no room for relativistic mass there.

The definition of relativistic mass is "a different mass ($\gamma m$) so that Newtonian formula (e.g $p=mv$) work in regions where Newtonian formula don't work". Definitely sus.

The relevant Minkowski space things are:

$$ u_{\mu} = (\gamma c, \gamma \vec v) $$

(Note: $\gamma$ is already here, and mass is not). Then

$$ p_{\mu} = mu_{\mu}$$

(note: looks like a generalization of $\vec p = m\vec v$...is that not good enough?).

$$p^2 = m^2|u|^2 = (mc)^2 $$

We're done: no relativistic mass.

You can also write:

$$ p_{\mu} = mu_{\mu} = (\gamma mc, \gamma m\vec v)$$

and then call that:

$$ p_{\mu} = (E/c, \vec p) $$

with

$$ E = \gamma mc^2 $$ $$ \vec p = \gamma m \vec v$$

and then have the urge to do:

$$ m \rightarrow \gamma m $$

so:

$$ E = mc^2 $$ $$ \vec p = m\vec v $$

at all $v$, but that has nothing to do with Minkowski space.

Answer 3

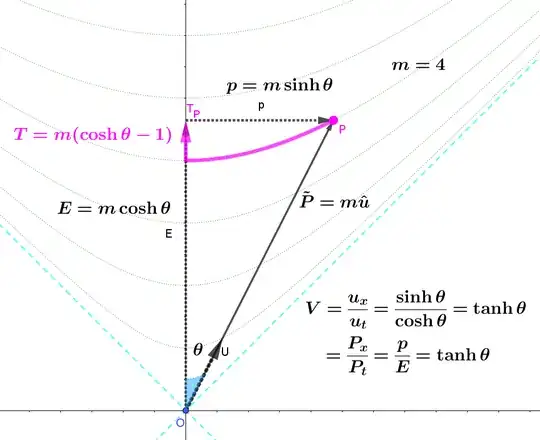
For a visualization, you might look at the mass-shell on an energy-momentum diagram.

From my answer to How is the time-component of the spacetime interval in a spacetime diagram related to the time component of the energy-momentum 4 vector?

Go to the referenced page for further discussion, including a discussion on "taking limits".