In this image, someone told me that there is no current flow through the 6 ohm resistor. Why not? Won't there be any flow till point E as well? If no, does the current choose one path to flow through over another?
FYI, this diagram has been provided in the book.
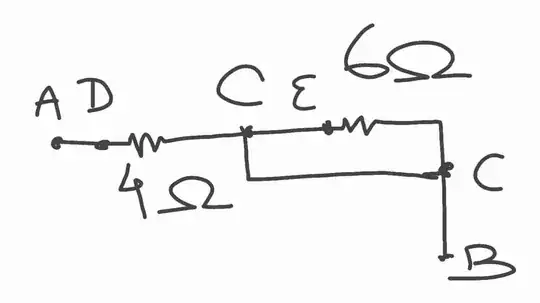
The 6 $\Omega$ resistor is shorted by the wire and current takes the path of least resistance, that is through the wire.
Alternatively, the combined resistance of the 6 $\Omega$ resistor and the wire CC (assumed perfect with resistance $0 \; \Omega$) is
$$R_{effective} = \frac{ 0 \; \Omega \times 6 \; \Omega }{ (0 + 6) \; \Omega} = 0 \; \Omega .$$
Referring to the wire as "the $0 \; \Omega$ resistor": Because the $6 \; \Omega$ and $0 \Omega$ resistors are in parallel, the potential difference (pd) across them is the same: this can be calculated as effective resistance $\times$ current. The current through the effective resistance is the current that flows through the $4 \; \Omega$ resistor. Since the effective resistance is zero, the pd across the $6 \; \Omega$ resistor is zero: No current flows through the $6 \; \Omega$ resistor, it all flows through the wire.
This fits with what is happening with the wire: Since the wire has zero resistance, the pd across it is (as well) zero.
