The observable universe has expanded over time due to the expansion of space. In the early universe, the observable radius was much smaller because light hadn't had as much time to travel and the universe was denser. The rate at which the universe expands is described by something called the scale factor, denoted by $a(t)$, which changes as the universe evolves. The formula for the radius of the observable universe at any point in time is:
$$
R_{\text{observable}}(t) = c \int_0^t \frac{dt'}{a(t')}
$$
Here, $c$ is the speed of light, $a(t)$ describes how fast the universe is expanding, and $t$ is the age of the universe.
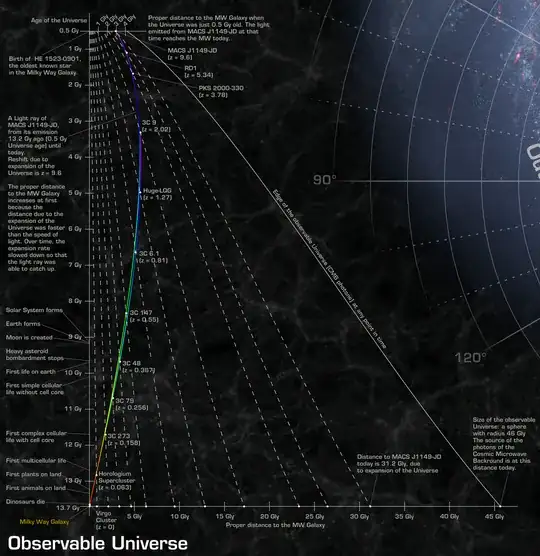
source
The observable mass refers to all the matter and energy within the observable universe, which is contained in a sphere with a radius equal to $R_{\text{observable}}(t)$. To figure out the observable mass at any given time, we multiply the average energy density $\rho(t)$ by the observable volume $V_{\text{observable}}(t)$ :
$$
M_{\text{observable}}(t) = \rho(t) \cdot V_{\text{observable}}(t)
$$
Where $\rho(t)$ is the average density and $V_{\text{observable}}(t)$ is the volume of the observable universe, calculated as:
$$
V_{\text{observable}}(t) = \frac{4}{3} \pi R_{\text{observable}}(t)^3
$$
In the early universe, radiation dominated. As the universe cooled down and expanded, matter took over as the dominant form of energy. Today, and dark energy is the main player.
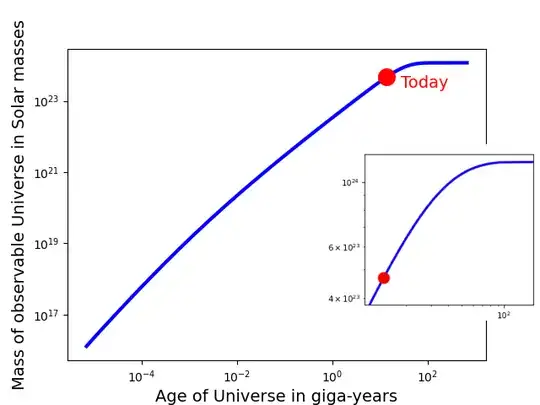
source unit of mass in this plot is $M_\odot \approx 1.989 \times 10^{30} \, \text{kg} $
Example [Approximation]
1.Today $t_0 = 13.8$ billion years:
At the present time, the scale factor is $a(t_0) = 1$. Using the simplified formula:
$$
R_{\text{observable}}(t_0) = \frac{c \cdot t_0}{a(t_0)} \approx 46.5 \, \text{billion light-years}.
$$
The average mass-energy density of the universe today is approximately $\rho_0 \approx 9.2 \times 10^{-27} \, \text{kg/m}^3$.
The observable volume at present is:
$$
V_{\text{observable}}(t_0) = \frac{4}{3} \pi R_{\text{observable}}(t_0)^3 = \frac{4}{3} \pi (4.4 \times 10^{26})^3 \approx 3.6 \times 10^{80} \, \text{m}^3.
$$
Now the total mass within the observable universe:
$$
M_{\text{observable}}(t_0) = \rho_0 \cdot V_{\text{observable}}(t_0) = 9.2 \times 10^{-27} \times 3.6 \times 10^{80} \approx 3.3 \times 10^{54} \, \text{kg}.
$$
2. Early universe $t = 1$ billion years:
At $t = 1$ , we approximate the scale factor as:
$$
a(t) = \left( \frac{t}{t_0} \right)^{2/3} \quad \text{(for a matter-dominated universe)}.
$$
For $t = 1$ and $t_0 = 13.8$ :
$$
a(t) = \left( \frac{1}{13.8} \right)^{2/3} \approx 0.27.
$$
Now, we calculate the observable radius at $t = 1$:
$$
R_{\text{observable}}(1 \, \text{billion years}) = \frac{c \cdot t}{a(t)} = \frac{3 \times 10^8 \, \text{m/s} \cdot (1 \times 10^9 \, \text{years})}{0.27}.
$$
Converting to light-years:
$$
R_{\text{observable}}(1 \, \text{billion years}) \approx 37 \, \text{billion light-years}.
$$
At $t = 1$ , the average density was higher due to the smaller volume. Let's assume the density was approximately $1000$ times higher, so:
$$
\rho(1 \, \text{billion years}) \approx 1000 \times \rho_0 = \mathcal{O}( 10^{-24} \, \text{kg/m}^3).
$$
The observable volume is:
$$
V_{\text{observable}}(1 \, \text{billion years}) = \frac{4}{3} \pi (R)^3 \approx \mathcal{O}(10^{77} \, \text{m}^3).
$$
The total mass at $t = 1$ is:
$$
M_{\text{observable}}(1 \, \text{billion years}) \approx \mathcal{O}(10^{53} \, \text{kg}).
$$

