How can spatial dimensions both expand and contract for the same observer at the same time?

Question

Suppose a lamp emits a single wavelength (monochromatic light).

The wavelength is A meters.

Next to the lamp lies a stick, also of length A.

Now we drive by the lamp at constant speed v, and then the stick, in that order.

We observe that the wavelength is now longer than A (red-shifted).

We observe that the stick is now shorter than A (length-contracted).

Somehow, two physical dimensions have changed size in opposite directions, along the same axis.

Is there a paradox here? How can simple measurable things both expand and shrink in the same space, for the same observer?

---

For reference:

When you move away from a light-source the frequency drops. However c = λ*f stays constant.

Therefore lambda must increase by this amount, known as red-shifting:

λ-red-shifted = λ-original * sqrt((c + v)/(c - v))

The length of the stick contracts by this amount due to v:

stick-shortened = stick-original * sqrt(1 - v^2/c^2)

Answer 1

You might as well ask how the Doppler effect can cause the shortening of the wavelength of sound at non-relativistic speeds where there is no length contraction! Length contraction and the Doppler effect are unrelated phenomena, so there is no contradiction between them. Length contraction is a geometrical property of spacetime which causes spatial distances to be frame-dependent. Your mistake is assuming that the Doppler effect is the result of length contraction, which it is not.

Addendum

Length contraction applies where you have two points, fixed relative to each other in their own rest frame, moving at some speed v through your frame, where v is less than c. You seem to be assuming that applies to a wavelength of light, which is nonsense. A wavelength of light is not two fixed points moving at a speed v.

Answer 2

Here's a spacetime diagram that models your scenario.
It's drawn on “rotated graph paper” so that we can count the ticks along segments.

Suggested by my comment to the OP, there is a distinction of these lengths:

• The observed-length of an object (like a ruler) is the measured spatial separation between
  parallel timelike-lines (the worldlines of the front and back of the object).

• The observed-wavelength of a light wave is the measured spatial separation between
  parallel lightlike-lines (associated with two successive signals received from a periodic source).

Below is a situation where the source observer emits a signal with a period of 10-ticks so that
the wavelength [the spatial separation between lightlike-signals] is $$\lambda_{source}=c(10 {\rm ticks})= 10\ \mbox{space-ticks} = 10 \mbox{ sticks}.$$ He obtains a ruler whose proper-length [the separation between parallel timelike-worldlines of the ruler ends in the rest frame of the ruler] is $L_{stick}=10\ \mbox{sticks}$, which was chosen to be equal to that wavelength $\lambda_{source}$.

In the source frame, an inertial receiver has velocity $v=(3/5)c$, as shown.
What does that receiver measure for the wavelength and for the ruler-length?

We construct the spatial-axis of the moving inertial receiver.

We note that for $(v/c)=(3/5)$, we have $\gamma=\frac{1}{\sqrt{1-(v/c)^2}}=5/4$ and $k=\sqrt{\frac{1+(v/c)}{1-(v/c)}}=2$.

As the receiver approaches the source, the receiver measures

• an apparent ruler-length of 8 sticks, ($(L/\gamma)=(10/(5/4))=8$)
  as represented by OL (the spatial separation of the ruler-worldlines)
• a wavelength of 5 sticks,
  as represented by OW' (the spatial separation of the successive lightlike-signal-lines)
  that are measured by the receiver during the approach.
  The approaching receiver encounters the backward-directed signals.
  
  Note the receiver measures a period of 5 ticks,
  so the ratio of periods $T_{obs}/T_{src}=5/10=1/2$,
  and thus the ratio of frequencies $f_{obs}/f_{src}$ is 2… blueshifted.

After the receiver passes the source and is now departing the source, the receiver measures

• an apparent ruler-length of 8 sticks, ($(L/\gamma)=(10/(5/4))=8$)
  as represented by OL (the spatial separation of the ruler-worldlines)… indeed $\gamma$ is an even function of $v$.
• a wavelength of 20 sticks,
  as represented by OW (the spatial separation of the successive lightlike-signal-lines)
  that are measured by the receiver during the departure.
  The departing receiver encounters the forward-directed signals.
  
  Note the receiver measures a period of 20 ticks,
  so the ratio of periods $T_{obs}/T_{src}=20/10=2$,
  and thus the ratio of frequencies $f_{obs}/f_{src}$ is 1/2… redshifted.

So, I think his apparent paradox is based on a misconception that does not recognize the distinction between the length of an object and the wavelength of a light wave.

(The diagram above is a variant of the one I made for my answer to Deriving Relativistic Doppler Effect through length contraction )

Here's a spacetime diagram for the receiver's frame.
I've included the worldline of the receiver's 10-stick ruler to help show the symmetry of length-contraction.

Answer 3

Just to give you a partial answer that I hope is somewhat instructive, I want to point out that length contraction doesn't always happen in relativity, and especially with moving objects.

And one of your objects, is light: it is the thing that can't stop moving, in this theory.

Suppose that I am in a spaceship occupying some inertial reference frame and I think that there is a space rock moving past me that is 1 km long. And it is zooming by at $\gamma = 2$ and I have to clarify that it is 1 km long in my frame of reference, but due to length contraction it is 2km long in its frame.

Now you come along with $\gamma=2$, what do you see?

Well, it depends on which direction you're going!

If you're coming in opposed to the motion of the rock, then to you it contracts further, looking (2/7) km long. Note that if I furnished a 1km measuring stick that happened to be instantaneously next to the rock for me (but stationary), it would on your account be significantly longer than the rock, 0.5 km as compared to 0.28 km, as it wouldn't get contracted by as much.

But if you're coming in moving in the same direction as the rock, for you it de-contracts to its rest length of 2 km, meanwhile my measuring stick is still only 0.5 km long.

This is all to say that if you were thinking of some sort of homogeneous isotropic length contraction, that's definitely not what we're describing here!

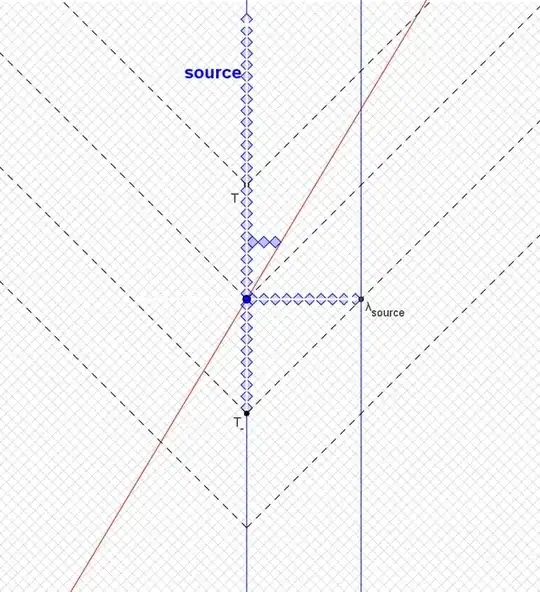
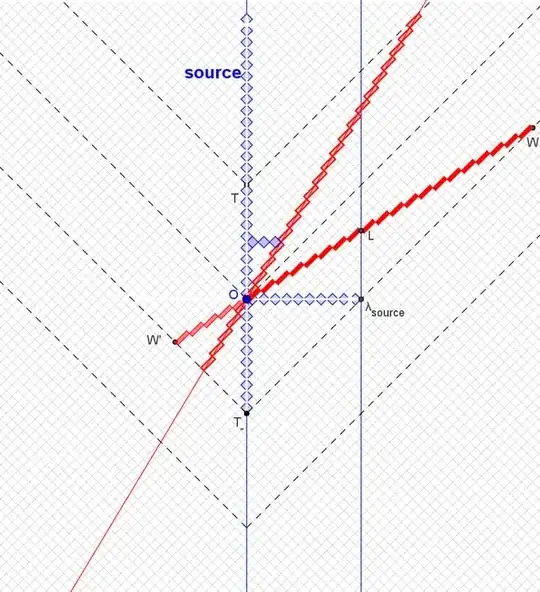
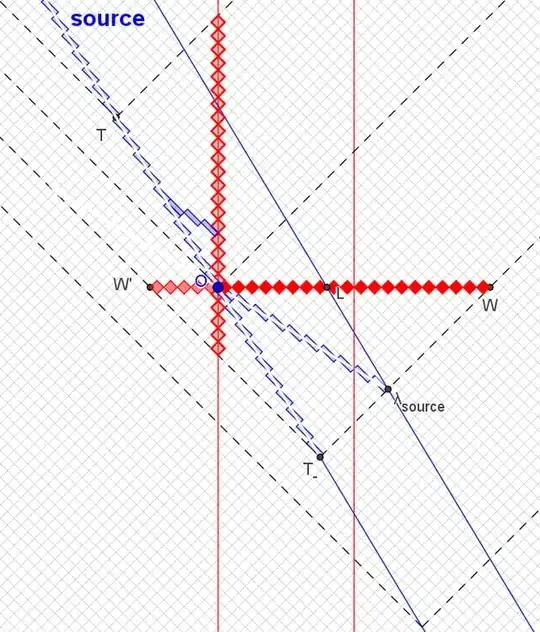
In terms of actually understanding it, I think different students require different insights before they suddenly “get it.” For me the insight was that the two edges of a rigid body form parallel lines on a spacetime chart $x$ vs $w=ct$, and those do Lorentz-transform to other parallel lines, and as they “tilt” they kind of “crowd together” while as they “untilt” they spread apart, this felt very unintuitive. But my “aha” that made it all click for me, was to look in the rest frame where the two lines are maximally un-tilted, they are in the $\hat w$-direction. And then I thought, “because of the relativity of simultaneity, moving observers have a present which is not in the $\hat x$ direction, and so they draw the diagonal line of “now” between these two lines at some angle, why don't they see the distance between the two as longer?” So the diagram that makes it click for me looks like this:

And the question is, why isn't that dotted blue line longer than the, in this case, 4 units between the two lines. And that is entirely due to the Lorentzian shape of the metric, it's $$\Delta s^2 = \Delta x^2 - \Delta w^2,$$ so the diagonal in this direction actually reduces the measured length commensurately.

So that meant a lot to me and probably doesn't mean so much to you! But just keep working problems in relativity and you will eventually find a perspective that clicks.

Answer 4

Consider this diagram: three wavelengths of a photon. Let the bottom rod (green) be at rest relative to the observer, and the top rod (blue) be moving with $\gamma=1.5$, contracting it to two-thirds of its original length. The photon is not redshifted at all here.

Note that, measured by the contracted rod (or measured by us if the light source and contracted rod are comoving/if we are moving past the light source and rod at relativistic speed), the photon’s frequency has decreased: over the same distance (one rod), the photon oscillates only twice as opposed to three times. This equates to redshift: as measured with the contracted rod (or as measured with a regular rod and a fast-moving light source), the frequency goes down and the wavelength goes up.

---

This is not a perfect representation - it wasn’t meant to be. But it does show that redshift and length contraction are due to the same phenomenon and can, without issue, appear together.

Answer 5

For an observer who is in rest relative to the stick, the phase of the light wave is the same at both ends of the stick.

However, for an observer who moves relative to the stick, the phases will not be the same because of the relativity of simultaneity.

Likewise, if the stick oscillates side-wise, for the moving observer it will be wavy, not straight.

Answer 6

You can make a similar "paradox" with baguettes. If you take a baguette and slice it one way you can get slices about 6 cm long. If you slice it another way you can get slices about 60 cm long. And if you slice it diagonally you can get baguette slices of any length in between.

In spacetime an object which is moving at some non-zero velocity is oriented diagonally. The faster it is moving the more diagonal it is. Length contraction is the disagreement on the length of the object due to slicing it on a spacetime diagonal.

Now, if you have several baguettes laid out on a table at different angles, and you cut all of the baguettes with one long straight knife, then you will get different sized slices. If you change the angle of the knife then some slices may get bigger and some slices may get smaller. This is geometrically the same as the issue you describe in your question.

So, yes, some slices will get longer and other slices will get shorter, depending on the angle (velocity) in the original frame. This is a little weird, but it is a feature of ordinary Euclidean geometry too. The main difference is that in spacetime the diagonal slices are shorter rather than longer.