1

Well,I know (and was also told) Newton's third law is just conservation of momentum in disguise.

And momentum is only conserved in a system when $\sum F_{ext}=0$.

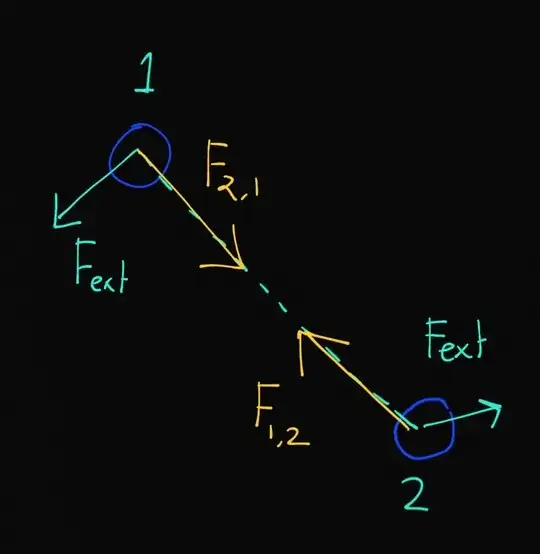
Alright,suppose there is a system of 2 particles in free space and they are interacting with each other via forces.Say I put an external force on both the particles in some direction.So,the momentum of the system : ( of 2 particles ) is not conserved.

figure

But,

Newton's third law is just conservation of momentum in disguise.

As momentum is not conserved here,does that mean $F_{1,2}\neq -F_{2,1}$?

$F_{i,j}$ indicates the force of particle $i$ on particle $j$.

Qmechanic
  • 220,844
epicpubgplayer
  • 422

4 Answers4

3

No, the third law is alway valid, and it implies momentum conservation when there are no external forces. If you enlarge your system to include the objects that apply those external forces, then the total momentum of the enlarged system will be conserved, because you will need to include the reaction to those "external" forces that are now inside your system.

Pato Galmarini
  • 2,675
2

Does Newton's 3rd law hold true everytime?

The answer to the title of your post is no. While it holds for most forces, it does not in all cases. An example is magnetic forces. But it does hold for your example.

By definition conservation of momentum only applies when the net external force applicable to the momentum underconsideration is zero. What you can say is that in the absence of a net external force it follows from Newton’s third law that momentum is conserved. That's because the Newton third law force that each particle exerts on the other becomes the net external force acting on the other particle.

Then, from Newton's second law, which states that the net force acting on a particle equals its rate of change in momentum, the rate of change in the momentum of each particle due to the force exerted on it by the other particle, is the same. .

In your two particle system the Newton third law pair of forces are internal to the system. Those forces are equal and opposite regardless of whether or not the net external force is zero. In other words Newton’s third law applies regardless of whether or not momentum is conserved.

Hope this helps.

Bob D
  • 81,786
1

Newton's third law is just conservation of momentum in disguise.

In the case where action-reaction pairs are net forces between bodies, we can say that conservation of momentum implies Newton's third law: $$\vec{F_{12}} = \frac{\vec {dp_2}}{dt}$$$$\vec{F_{21}} = \frac{\vec{dp_1}}{dt}$$ When $$\frac{{d(\vec{p_1} + \vec{p_2})}}{dt}=0 \implies \vec{F_{12}} + \vec{F_{21}} = 0$$ But if momentum is not conserved, it doesn't follow that the action reaction pair is not equal in modulus and opposite, as required by Newton's third law. It is possible that they are not net forces, as in your picture.

Because third law is more than conservation of momentum. The action reaction pair: my downward force on the chair and the upward force of the chair on me has nothing to do with conservation of momentum. It is a postulate of mechanics that those forces are equal in modulus and opposite.

Claudio Saspinski
  • 17,607
-1

The usual way to think about this is that there are internal interactions between particles within the system, and there are external interactions between particles and the environment. The internal interactions are always conservative, even if the external ones are not.

In this case, the forces $F_{1,2}$ and $F_{2, 1}$ are internal interactions, and thus are conservative.

Cort Ammon
  • 53,814
  • 6
  • 103
  • 176