1

Vacuum fluctuations exist even in a perfect vacuum. In the Casimir effect, wave frequencies greater than the distance between closely spaced grounded metal plates are mostly excluded from the space between plates. The Scharnhorst effect essentially predicts that because the density of waves between the plates is less, light will move faster than the general speed of light in a vacuum.

  • First, shouldn't the result also be true of nano-scale holes in a grounded piece of metal?

  • In which case, a bank of parallel metallic carbon nano-tubes should work for testing, right?

  • Third, can we generate long enough straight tubes (or a series of banks of tubes) to test for a deviation in light speed?.

Hence the title question.

Brian Gridley
  • 119

1 Answers1

0

This is a comment but its best demonstrated via photo so I am attaching as an answer.

Note the scharnhorst effect is an increase in speed NORMAL to the direction of the plates. That is the photon bounces back and forth between plates faster, not travels down the space of plates faster. So the carbon tubes for your question don't have to be extremely long to test the effect (well maybe they need to be long because the effect is still small), instead you want the photon to enter your tube at a very sharp angle so that it bounces back and forth as much as possible. And in the event the Scharnhorst effect it will bounce MORE than usual amounting to a kind of refraction.

I.E. Assuming a regular speed of light we might expect the following:

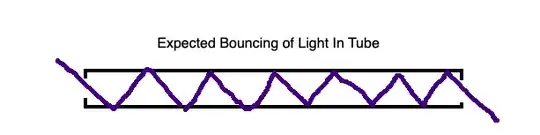
Regular light path in tube

But the Scharnhorst effect by "increasing the speed normal to the plates" instead results in

Scharnhorst path in tube that bounces back and forth faster

Where both paths take equally long to traverse across the length of the tube, just the Scharnhorst path covers a longer distance.

In both those images you should assume the purple light enters at the "same angle".

In a certain sense, if you can get the angles to line up right, the Scharnhorst effect would send the exiting light in a totally different direction than if the Scharnhorst effect had not been there. That would perhaps be the easiest way to test it. But the sharpness of the angle OR length of tube to pull this off would need to be extremely-precise and enormous respectively.

The alternative is to keep the tube short but have a precise way of counting how many bounces occurred, or simply how much distance did the light travel.

But the latter is subtler point than meets the eye. We take for granted the speed of light is $c$ and so we have fixed expectations on how the phase of our light changes as a function of how far it has travelled and these can be used to compute how the phase changes depending on how long it has travelled.

Since the Scharnhorst effect breaks that constant relationship between distance and time for light, one should ask “does the phase couple to the time or the distance? Those are different things now”.

I’m sure someone legitimately competent at QED (which I’m not) would be able to answer these sorts of questions.

Sidharth Ghoshal
  • 3,041