Is the person in the picture doing any work?

Question

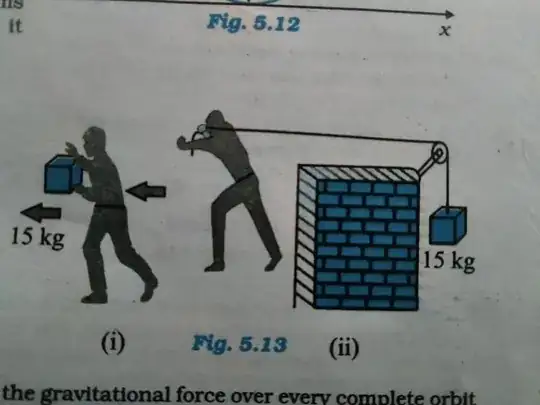
"In figure (i) the man walks 2m carrying a mass of 15kg on his hands. In figure (ii) he walks the same distance pulling the rope behind him. The rope goes over a pully and a mass of 15kg hangs at its other end. In which case is the work done greater?"

Answers to this question on the internet say that since in figure (i) he applies force upward to lift the box up, and pushes the block forward, force is perpendicular to displacement and he does zero work. But does he not also apply force in the forward direction to push the box? Why do we neglect that force? What is the actual work done by man(i) on the box and how much is it?

Answer 1

During the process of accelerating, he will indeed have to apply a horizontal force. However, once he is up to speed, he can continue moving that way indefinitely without any more expenditure of energy. For better or for worse, problems in textbooks do things like assume the man is already moving at a constant velocity and ignores the acceleration bit.

Also, in theory the person can reclaim the energy spent accelerating when they decelerate back to a stop. This is the foundation for regenerative breaking.

Answer 2

The simplest case is when only one force is applied to an object at rest. The force accelerates the object, increasing its velocity and giving it kinetic energy. This is called doing work on the object. The acceleration, velocity, and displacement are in the direction of the force. The work done can be shown to be $W = F\cdot d$.

If the object has a sideways velocity, the object will move sideways as the force does work. The force does not change the sideways velocity. It adds nothing to the kinetic energy gained. The work done is unchanged.

Examples are gravity doing work on a dropped object or a spring pushing an object.

The opposite is when a force slows a moving object. In this case, the velocity and displacement are in the opposite direction to the force. The acceleration is always in the direction of the force. Kinetic energy is converted to potential energy. This is called work done by the object. $W = F \cdot d$.

Again, sideways displacement has no effect on the loss of kinetic energy.

Examples are the opposite of the previous ones. Work is done by an object throw upwards as gravity slows it. It is done as a moving object compresses a spring.

Choosing two very similar names for two very similar ideas was not the best choice.

Answer 3

The human body is a terrible choice for learning the fundamentals of mechanics. Most examples use blocks, springs, rollers, etc to reduce the scenario to its basic elements. So, if you're confused by this example, do not feel too discouraged.

In this case, yes the man in (i) is doing significantly less work than the man in (ii), but not "no work" unless we implicitly neglect the stepping motion of his legs, the internal structure of his muscles and how they apply force, and the horizontal work he needed to do to accelerate to a roughly constant speed.

Replace the man with the Mars Curiosity Rover, which has a table-like structure and moves using treads, in both cases, and the situation becomes more clear.

Answer 4

Here is how I would summarise -

Case 1: Horizontal Motion at Constant Velocity Scenario: The man is carrying a 15 kg box horizontally at a constant velocity. Work Done: 0 Joules The force exerted by the man (upward to counteract gravity) is perpendicular to the direction of motion (horizontal). Since the angle between the force and displacement is 90 degrees, no work is done on the box.

Case 2: Horizontal Motion with Acceleration Scenario: The man is accelerating while carrying the 15 kg box horizontally. Work Done: Work = mass × acceleration × distance Here, mass is 15 kg, acceleration is the horizontal acceleration, and distance is the distance moved. Work is done on the box as the man exerts a horizontal force to accelerate it, which increases the box’s kinetic energy.

Case 3: Vertical Motion with Acceleration (Using a Pulley) Scenario: The man is pulling the 15 kg box upward with a pulley, and the box is accelerating upward. Work Done: Work = Fm × distance Here acceleration is the upward acceleration, and distance is the distance the box is lifted. The work done includes both the increase in potential energy (more accurately Earth Block system) due to lifting against gravity and the increase in kinetic energy due to the upward acceleration.