The size of elementary particles

Question

There is no evidence that particles like electrons have inner structure.

The question is, when people say that electrons are point-like do they mean:

1. If we measure an electron to be localized to within x meters of size we have the electron localized to within x meters of size. Ie, the electron is as small as the experiment designed to measure its size but no evidence it is point-like.

2. We do have evidence the electron is point-like, ie, we have evidence of a property that is not displayed by any particle that has a size. Only a particle with no size could have this property.

If it is the second case, what is that evidence?

Answer 1

In addition to the good answer by @JEB, a bit more information can be added to help understand the issue. The important feature that demonstrates that a particle is a point particle is Bjorken scaling. It shows that there is a scaling invariance in the scattering data when performed over a range of energies.

In the case of the proton, which has a substructure and a finite size, this scale invariance breaks down at energies that are comparable to the scale associated with its mass (which is related to its size). It thus reveals that the proton is not a point particle. For the electron, Bjorken scaling remains intact up to scale far exceeding the scale of its mass. As a result, it is concluded that the electron is a point particle.

Answer 2

We measure a particle's size by plastically scattering a point particle off it, e.g., to measure the protons size, we do:

$$ e^- + p \rightarrow e^- + p $$

and look at the cross section versus momentum transferred to the target ($|q|$).

You then compare it to the formula for point particle scattering (Mott scattering)

$$ \sigma = \sigma_{Mott} F(q^2) $$

and get a nice figure:

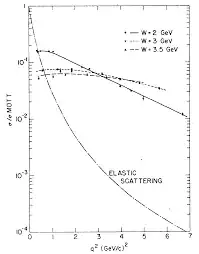
where all we care about is the smooth curve labeled "ELASTIC SCATTERING".

Note that:

$$ \hbar c = 0.2\,{\rm GeV\cdot fm}$$

so the figure here goes to $7\,(GeV/c)^2$m so it probes distances down to:

$$ L = \frac{\sqrt{7\,(GeV/c)^2}}{\hbar c} \approx 10^{-16}\,{\rm m}\approx R_{proton}/10 $$

Moreover, $F(q^2)$ (called the Elastic form factor) is the Fourier transform of the radial charge distribution (which is spherically symmetric for the proton). so elastic scattering measures the charge distribution of the target particle. (There is also one for the magnetic dipole distribution).

For electrons:

$$ \rho(r) = \delta(r) $$

so far. Idk what the current limit is for electrons, but it's much smaller than the proton radius. There is no sign of of structure for any of the quarks or leptons.

Note that pion and photon form factors have been measured. The latter is possible because photons have hadronic content via the $\rho^0$ meson.

Answer 3

Experimentally a point particle is identified by the way that it scatters other particles. A point particle has a characteristic scattering as shown by Rutherford.

When we measure a departure from the Rutherford scattering signature, the point of departure indicates the size of the particle.

http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/rutsca3.html#c4

Point particles follow the Rutherford curve for all non-relativistic energies, or the Mott curve for relativistic collisions. Our currently available data is limited by the highest energy collisions we can produce. So indeed, some particles that currently are classified as point particles may turn out to deviate from the curve at currently inaccessible energies.

Answer 4

I would say the physical electron is not a point particle as it has the Coulomb field and vacuum polarization, which I believe are part and parcel of the physical electron. Dehmelt said: "an elementary Dirac particle, such as the electron, is the closest laboratory approximation of a point particle." So when people say that the electron is a point particle they mean (or should mean) that it is described very well by the Dirac equation / quantum electrodynamics, and quantum theory implies the uncertainty principle, i.e. uncertain position, rather than vanishing size.