Important background: In the Clausius–Clapeyron equation, $\frac{\Delta P}{\Delta T}$ refers to the slope of the equilibrium phase-change coexistence curve, not necessarily to any actual pressure and temperature shifts at any time in any given problem. (I think you reason this out in your last paragraph.) For this reason, I recommend typographically distinguishing it as, say, $\frac{\Delta P^\star}{\Delta T^\star}$ or $\left.\frac{\Delta P}{\Delta T}\right|_\mathrm{solid–liquid}$ to reduce ambiguity. Again, $\Delta P^\star$ and $\Delta T^\star$ refer to coupled shifts in phase-change conditions, not necessarily in system conditions.
Reif's problem 8.8 is as follows:
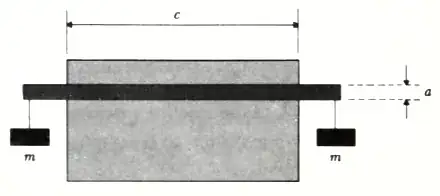
A steel bar of rectangular cross section (height a and width b) is placed on a
block of ice with its ends extending a trifle as shown in the figure. A weight of
mass m is hung from each end of the bar. The entire system is at 0°C. As a
result of the pressure exerted by the bar, the ice melts beneath the bar and
refreezes above the bar. Heat is therefore liberated above the bar, conducted
through the metal, and then absorbed by the ice beneath the bar. (We assume
that this is the most important way in which heat reaches the ice immediately
beneath the bar in order to melt it.) Find an approximate expression for the
speed with which the bar thus sinks through the ice. The answer should be in
terms of the latent heat of fusion I per gram of ice, the densities ρi and ρw of
ice and water respectively, the thermal conductivity k of steel, the temperature
T (0°C) of the ice, the acceleration due to gravity g, the mass m, and the
dimensions a, b, and c, where c is the width of the block of ice.
When the weight of the newly added bar augments the atmospheric pressure by $\Delta P^\star=\Delta P$—an actual change—it's the equilibrium ice melting temperature that decreases according to $\Delta T^\star = \frac{\Delta P^\star\Delta v T}{L}= \frac{\Delta P\Delta v T}{L}$, and this shift can be minimal relative to $T_0$. (Indeed, the problem is written to assume that it's minimal.) Additionally, temperatures must be continuous across interfaces. Since the ice in contact with the bottom of the bar is now above its melting temperature, it melts, absorbing latent heat $L$. This endothermic process cools the interface and surrounding region, as mediated by the material and geometrical properties of the setup, some of which are unspecified, as you note.
The newly obtained liquid water, as a fluid, is squeezed out of the way of the heavier steel above. When the interface has cooled to $T_0-|\Delta T^*|$, rapid melting stops. A temperature gradient through the steel (stated to be the predominant heat transfer mechanism) is coupled by Fourier's law to heat flow, which is supplied by the exothermic freezing of readily available liquid water into ice at the top of the bar. (Why does it freeze? Because the bar below is tending to cool below 0°C.) Reif's figure illustrates this new stage of slow, steady downward movement:
The phase changes occur close to equilibrium. (I review the extremely rapid kinetics of phase changes here.) The fluid movement is faster still. If the ice directly below the bottom of the bar were any colder than $T_0-|\Delta T^*|$, it wouldn't melt; if it were any hotter, it would melt nearly immediately. Similarly, if the liquid water at the top—at atmospheric pressure—were any colder than $T_0$, it would freeze nearly immediately. This fixes the actual temperature drop $\Delta T=\Delta T^\star$ vertically through the bar for the purposes of solving this problem. It's because the movement is so slow that the Clausius–Clapeyron slope—an equilibrium relation—can be used to approximate the actual system behavior.
What about ice near the bottom of the bar? Its pressure $P^\prime$ is lower than $P_0+\Delta P$ because ice, being a solid, dissipates localized stress fields with increasing distance. Its temperature must be lower than the corresponding Clausius–Clapeyron $\Delta T^{\prime\star}$ shift for that particular pressure shift $\Delta P^{\prime\star}=P^\prime-P_0$, or it would melt. (And of course, its temperature must also be above $T_0-|\Delta T|$ because it's always been surrounded by the same phase at temperatures higher than that.) So I don't agree with the question's statement that "The bottom part, for example, constantly alternates between contact with melted ice at temperature $T(p_b)$ and new solid ice at temperature $T_0$." A more nuanced look at the spatial temperature variation is necessary than idealizing it as discrete jumps. And remember that the problem states that no part of the ice or steel strays notably from 0°C.
What about liquid water moving around the bar to the top? It ultimately warms from $T_0-\Delta T$ to $T_0$ before freezing. Could it freeze along the way? Conceivably, but the problem states that it freezes at the top of the bar.
Is (sensible) heat transfer occurring throughout the ice and water? Yes. But Reif instructs us specifically that that this heat transfer isn't kinetically limiting the sinking of the bar—that it's conduction through the bar that dominates the kinetics. This is why the specific heat capacity of the water, for example, doesn't appear in the final relation.
In summary, I think you're right to examine the question and assumptions as carefully as you have. There's one "obvious" way to combine all the given variables (and no others) into a speed, but that doesn't mean it's appropriate to skim the problem statement and just write down a dimensionally correct answer (and you didn't). There are many reasonable questions that could be raised as to what's going on in all regions and interfaces here, and hopefully you can now appreciate how carefully the problem was constructed to send the reader in the direction of the intended analysis.
Does this resolve the issue(s)?
