I had already edited this question in response to the criticisms of those who closed its first version, as described in my comment below following the first group of others' comments. Perhaps I neglected to check the box indicating that the edited post was to be reconsidered for reopening. If the following, already edited first paragraph doesn't clarify what my question is adequately, I won't try further to do so.
A black hole is said to be black because of its space-time structure. This puzzles me, because of the argument below, which seems to show that, because of time-reversal symmetry, since a small particle falling into a black hole is an event which obeys the laws of nature, a small particle climbing out of a BH is also an event that obeys the laws of nature, i.e., if the first type of event is a theoretically possible event, so is the second type of event. What is wrong with the following argument?
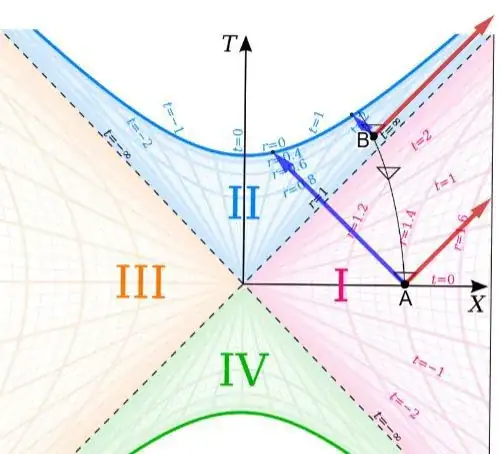
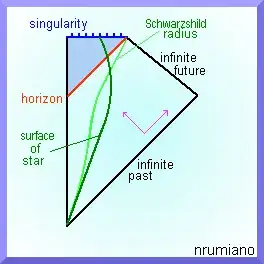
Consider as a black hole the object formed as a result of the gravitational collapse of a spherically symmetric, non-rotating, homogeneous cloud of pressureless, uncharged dust, as described in the Oppenheimer-Snyder paper "On continued gravitational contraction", which is a slightly less idealized model of a BH than the Schwarzschild BH model, which is time-independent. The final, after a finite time as measured in a coordinate system falling in with some portion of the dust, time-independent result of the collapse described in the O-S paper has, nevertheless, as shown by Birkhoff's theorem, the same S-T structure, outside of the singularity, as the Schwarzschild BH solution, whose line element defining the S-T metric is given by:
$ds^2 = (1-2M/r)dt^2 - 1/(1-2M/r)dr^2 - r^2(dθ^2 + cos^2(θ)dϕ^2)$ (1)
(letting c = G =1, and M be the mass of the BH), where $ds^2$ [= $(ds)^2$, not d($s^2$)] is the invariant (Lorentz) magnitude (squared) of the small space-time interval consisting of dt, dr, rdθ, and rdϕ where, outside the event horizon at r = 2M, dt is the magnitude of a small time interval, dr is the magnitude of a small radial (from the singularity) space interval, and rdθ & rdϕ are the magnitudes of small spatial intervals on a sphere centered at the singularity, with θ and ϕ being the angle coordinates of spherical coordinates, all measured by a distant ("at infinity") observer. Inside the event horizon, its not clear exactly what the significances of t, r, θ. and ϕ are, except they are the coordinates of the Schwarzschild solution, and, because the coefficients of dt and dr inside have the opposite sign to their sign outside the BH (where r > 2M), inside the BH, t is a spatial coordinate and r is the time coordinate. There are other coordinate systems for a BH, but all of them seem to be derived from the Schwarzschild solution and use its coordinates, or coordinates derived from them, except for infalling coordinate systems, and I was unable to find formulas for complete S-T coordinates of a BH in terms of infalling coordinates for a test particle falling all the way from outside the event horizon, through that, to the singularity, in one coordinate patch, using which would have avoided the perhaps questionable patching of interior B-H coordinates to exterior B-H coordinates to provide a unified B-H interior-exterior coordinate system. (The advantage of true infalling coordinates, that can describe any space-time point, not just coordinates that apply to an infalling particle, is that, although they are time-dependent, they eventually are referenced from a point at the event horizon of the BH, and later inside it, thus avoiding the problem of coordinates becoming singular at the event horizon.)
Since $dt^2$ = [$d(-t)]^2$, and $dr^2$ = $[d(-r)]^2$, the S-T metric of a BH is time-reversal invariant, i.e., its time reversal is itself. (Commonly, the S-T structure of the time-reversal of a black hole is said to be the S-T structure of a white hole, which is said to be different from that of a black hole, but I am unable to see the difference.) The S-T structure of the time reversal of a small (classical, non-QM) test particle falling into a BH, with the particle being too small to significantly affect the S-T metric of the BH, is thus the time reversal of that infalling particle in the S-T structure of the time reversal of the BH, which is the particle coming out of the S-T structure of the BH. Since the time reversal of each physical event which is possible according to the fundamental laws of the universe, except a few involving the weak force (and even there, PCT symmetry- the combination of the spatial parity operation, changing a particle into its anti-particle & vice-versa, and time reversal- holds, and a BH is invariant under P, i.e., P would change the S-T structure of a BH into the S-T structure of a BH, and according to recent experiments anti-matter behaves gravitationally just like matter, so a BH is invariant under C, so finally a BH must be invariant under T), is also possible according to those laws, we conclude that since a particle falling into a BH is possible according to the fundamental laws of the universe, a particle coming out of a BH is also possible according to the fundamental laws of the universe. This seems to contradict the usual wisdom that a BH is totally black, i.e., that nothing can come out of it (excluding, perhaps, Hawking radiation). It is unclear what is the structure of the interior of, so what exactly might go on inside, a BH, so it is difficult to base a convincing argument for the possibility of escape from that interior on any detailed dynamics there; an argument such as mine, based on time reversal (or PCT) invariance of a BH, avoids this problem, relying only on one of those holding for it.
[However, on p. 824, §31.3 of Gravitation, by Misner, Thorne, and Wheeler, there is a description which seems intended to be of a physically possible process. The description is: a test particle is ejected from the singularity INSIDE a BH, travels radially outward from r = 0 to r = 2M, crosses the event horizon, at r = 2M, going OUTWARD, goes to some turnaround point OUTSIDE the BH at r > 2M, thereafter fals back into the BH and eventually re-enters the singularity at r = 0. Here M,T,&W seem to be agreeing with me, that escape from the interior of a BH to its exterior is theoretically possible, although elsewhere in Gravitation they appear to claim that it isn't. I intend to study the details of this, but presently I am unable to account for it.
Also, my question was asked in PSE about 12 years ago, and received an answer (that got a net 64 upvotes) by John Rennie on May 14, 2012, link here, which may be quoted as an argument against my position, so I will answer it here. Rennie used the Gullstrand-Painleve coordinates of an infalling particle in his answer, and claimed to have shown that a black hole was black because nothing can escape from it. His argument was:
The line element of a radially infalling particle in G-P coordinates is given by:
$ds^2 = (1 - 2M/r)dt_r^2 - 2\sqrt{2M/r}dt_rdr - dr^2$ (2).
Rennie considers outgoing (!) light rays, for which $ds^2 = 0$. Thus, he says, we have:
$0 = (1 - 2M/r)dt_r^2 - 2\sqrt{2M/r}dt_rdr - dr^2$, (3),
where "$t_r$ is the light ray's proper time, for an outgoing light ray. He next divides through by $dt_r^2$ and rearranges, to give:
$-(dr/dt_r)^2 -2\sqrt{2M/r}dr/dt_r + (1-2M/r) = 0$,
which has the solutions
$dr/t_r = -\sqrt{2M/r} ± 1$.
Rennie says $dr/dt_r$ is the radial velocity in the G-P coordinates, with the -1 giving the velocity of the inbound light beam, while +1 gives the velocity of the outbound beam. At the event horizon, r = 2M, so the outbound velocity
$dr/dt_r = 0$,
so at the event horizon the outbound light velocity is zero, so light can't escape from the BH, so nothing can escape from it. In fact, for r < 2M, the outbound velocity of light is negative, so there light must move toward the singularity.
However, Rennie did the above incorrectly, as shown by the following:
First, a light ray has no proper time which can serve as a coordinate for points on its worldline. Light follows a null trajectory, whose tangent vector at all points is a null vector, so locally the invariant (Lorentzian) distance between any two points on it is zero, and so the travel time of a light ray moving between such points, as measured in the coordinate system of the light ray (which system doesn't exist, but taking the limit as measured in coordinate systems which approach the velocity of the light ray, as determined in some fixed coordinate system), is zero, so the proper times of all points on the light ray's world line, if they existed, would be the same. Thus, taking the derivative of r wrt the proper time $t_r$ ($dr/dt_r$) would involve taking the limit as Δr → 0 of Δr/0, i.e., a divide by zero fallacy.
Second, Rennie claims eq. (3) for outgoing light rays follows from eq. (2), but eq. (2) holds for infalling, not outgoing, particles.
Third, a correct calculation similar to Rennie's goes like this:
For a massive particle falling from infinity radially into a BH, which does have a proper time T, the ds in eq. (2) is equal to dT, and the $dt_r$ also turns out to be equal to dT. Thus,
$dT^2 = (1 - 2M/r)dT^2 - 2\sqrt{2M/r}dTdr - dr^2$,
and dividing through by $dT^2$ and rearranging gives
$(dT/dT)^2 = (1 - 2M/r)x1 - 2\sqrt{2M/r}dr/dT - (dr/dT)^2$, or
$(dr/dT)^2 + 2\sqrt{2M/r}dr/dT + 2M/r = 0$,
which has the single solution, of multiplicity 2,
$dr/dT = -\sqrt{2M/r}$.
Thus, at the event horizon, where r = 2M, dr/dT = -1, and for the time-reversed event, with dT' = -dT, indicating a particle climbing out of the BH, dr/dT' = 1. What this signifies is a bit peculiar. Outside of the BH, r denotes ordinary spatial distance, so dr/dT is just ordinary speed, in units of Schwarzschild coordinates per particle proper time, scaled to the speed of light being 1. Inside the BH, however, r denotes Schwarzschild coordinate time, so dr/dT is that coordinate time per particle proper time.]
The (mental, and other aspects of the universe) direction of increasing, forward time in the universe outside a BH, with the dinosaurs occurring before humans, is said to be because this is the temporal direction of increase of the entropy of the matter in the outside universe (although this has hardly been proven). Entropy increase inside a BH can't be taken as providing a temporal asymmetry there, since there is no matter inside a BH of which to have increasing entropy, except in the singularity, and that is a total unknown. (This is ignoring the QM-related BH entropy of Bekenstein and Hawking.) It might be objected that the temporal direction of entropy increase of an infalling object ought to somehow be considered in all this, but for a very simple small particle such as an electron, there is no entropy decrease or decrease (and likely the possibility of something coming out of a BH doesn't depend on whether it is an electron or instead, say, a human).
As for the fact that there is considerable observational evidence that matter can and does fall into the actual BHs that we have observed, and none that matter can come out of them, that hardly is good evidence that it is against the fundamental laws of nature for something to come out of a BH. We have observational evidence that asteroid-sized objects can and do fall into Jupiter, but none, as far as I know, that any observable matter comes out of it, yet it is not at all against what we consider the fundamental laws of nature that matter can (and probably does) come out of Jupiter.
The foregoing is not meant to (very) seriously argue that matter can come out of a BH, it is just an argument that, taken by itself, seems good to me, but that I think, judging by the weight of expert opinion, is probably faulty, but in ways that I don't see. The crux of my argument that the (non-quantum mechanical) physical laws of space-time allow something to come out of a BH is that the s-t structure of the time reversal of a BH, which BH's s-t structure is given by eq. (1), is also given by eq. (1), so is also the s-t structure of a BH. If this isn't true, what is the s-t, metrical structure of the time reversal of a BH?