Background
Rational zeta series are series of the form $$\sum_{n=2}^{\infty} q_{n} \zeta(n + p, m), \label{1} \tag{1} $$ where $\zeta(x,m)$ is the Hurwitz zeta function and $q_{n}, \ p \in \mathbb{Q} \setminus \{ 0 \} $ for all $n$.
Every real number $x$ can be expressed by means of such a series. For instance, we have $$ \sum_{n=2}^{\infty} \zeta(n,2) = \sum_{n=2}^{\infty} \left( \zeta(n)-1 \right) =1. \tag{2}\label{2} $$ Here, $\zeta(\cdot)$ is the Riemann zeta function. Also, we have $$ \sum_{n=2}^{\infty} \frac{(\zeta(n)-1)}{n} = 1 - \gamma, \tag{3}\label{3} $$ where $\gamma$ is the Euler-Mascheroni constant.
Zeta values in physics
Various values of the Riemann zeta function come up in physics. For instance, the Riemann zeta function at odd positive arguments arise in the correlation functions of antiferromagnetic XXX spin chain.
Also, the value $\zeta(4)$ comes up in the Stefan-Boltzmann Law. Moreover, the value $\zeta(3/2)$ comes up in the critical temperature of the Bose-Einstein condensate. Other physical interpretations of the Riemann zeta function $\zeta(n)$ for $n>1$ can be found over here.
In addition, the Riemann zeta function at the negative integer arguments also has relevance to physics. For instance, the value $\zeta(-1)$ bears relevance to bosonic string theory. Furthermore, the value $\zeta(-3)$ comes up in calculations in the context of the Casimir effect. More physical interpretations of the negative Riemann zeta values can be found in this MO question and this Physics SE question.
Rational zeta series at non-integer arguments
The paragraphs above provide examples of zeta values that come up in physics. In the context of this question, I am not interested in such isolated values, but in the rational zeta series described at the top. More specifically, I am interested in rational zeta series with non-integer arguments. What I mean by that, is that $p \in \mathbb{Q} \setminus \mathbb{Z}$ in equation \eqref{1}.
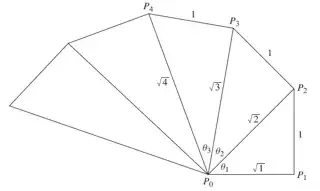
Examples of such series come up in the study of the Spiral of Theodorus. For instance, the Theodorus constant is described in equation (16) of the following paper (PDF) by David Brink:
\begin{align} T &:= \frac{1}{2} + \sum_{k=1}^{\infty} (-1)^{k+1} \left[ \zeta\left(k+ \frac{1}{2} \right) -1 \right] \tag{4} \label{4} \\ &= \sum_{x=1}^{\infty} \frac{1}{(x+1)\sqrt{x}}. \tag{5} \label{5} \end{align}
It is related to the sum of the internal angles of Spiral of Theodorus, depicted below:
Another example of a rational zeta series with non-integer arguments is Hlawka's Schneckenconstante (described on p. 2 of Brink's paper):
\begin{align} K &:= \sum_{k=0}^{\infty} (-1)^{k} \frac{\zeta(k+1/2)}{2k+1} \tag{6}\label{6} \\ &= \frac{\pi}{4} + \sum_{k=0}^{\infty} (-1)^{k} \frac{\zeta(k+1/2) -1}{2k+1}. \tag{7}\label{7} \end{align}
Questions
What rational zeta series at non-integer arguments (see equation \eqref{1} with $p \in \mathbb{Q} \setminus \mathbb{Z}$) come up in physics - if any? How and where do such series appear?