2

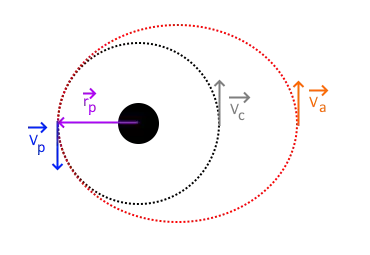
How can you determine the velocity at the apogee in a Hohmann transfer, given the radii of the initial circular orbit $r_p$, and the velocity change $\Delta v$ for the transfer? If I'm not mistaken, this should be enough information to determine the velocity $v_a$ at the apogee of the elliptical transfer orbit?

enter image description here

In the image: $\vec{v_c}$ is the velocity of the circular orbit with radii $|\vec{r_p}|$ and $|\vec{v_p}|=|\vec{v_c}|+\Delta v$. The black circle is earth or more generally a celestial body with gravitational parameter $\mu=GM$.

Here is my thinking:

Since the original orbit is circular, we can deduce the velocity of this orbit:

$v_c=\sqrt{\frac{\mu}{r_p}}$.The velocity at perigee in the new elliptical orbit is $v_p=v_c+\Delta v$.

If the radii of the orbit is given by $r(t)$, and we set the perigee to be at $t=0$, we now know $r(0)=r_p$ and $\dot{r}(0)=v_p$. We assume the only force acting on the satellite in this new orbit is gravity. This leads to a second order differential equation with two constants of integration. Since we know $r(0)$ and $\dot{r}(0)$, we can determine these constants. $\Rightarrow$ It should be possible to determine $v_a$.

Do you need to solve $F=ma=m\ddot{r}(t)=F_G=-\mu\frac{m}{r(t)^2}$? Or can you use other approaches? Could you somehow use one or more of these facts?:

  1. $T+V=E=$constant (kinetic energy + potential energy = conserved)
  2. $L=$constant (angular momentum conserved)
  3. Apogee is $180^\circ$ from perigee
  4. $r(t)$ is at it's maximum value at apogee and $\dot{r}(t)$ is at it's minimal value at apogee.

I kinda tried to use the conversion of energy, but you need to know the radii at apogee to do this. $T+V=\frac{1}{2}mv_p^2-\mu\frac{m}{r_p^2}=\frac{1}{2}mv_a^2-\mu\frac{m}{r_a^2} \Rightarrow \frac{v_p^2}{2}-\frac{\mu}{r_p^2}=\frac{v_a^2}{2}-\frac{\mu}{r_a^2}$.

Same for conservation of angular momentum: $|\vec{L}|=|\vec{p}|\cdot|\vec{r}|=m|\vec{v}|\cdot|\vec{r}|$. If we set the two points equal to each other we have two unknowns: $|\vec{v_p}|\cdot|\vec{r_p}|=|\vec{v_a}|\cdot|\vec{r_a}|$.

But using both energy conservation and conservation of angular momentum I now have two equations and two unknowns, which should be solvable.

So now I have this system of equations:

$$\begin{align} \frac{v_p^2}{2}-\frac{\mu}{r_p^2}&=\frac{v_a^2}{2}-\frac{\mu}{r_a^2}\\ v_p\cdot r_p&=v_a\cdot r_a \end{align}$$

and I also have this differential equation:

$$\ddot{\vec{r}}(t)=-\frac{\mu}{|\vec{r}(t)|^2}\mathbb{\hat{r}}$$

Is this correct? Am I on the right track here? Both of these approaches kinda seem excessivley difficult for the simplicity of the problem. Is there some simpler approach? If not, how do I solve the system of equations or the differential equation? I'm kinda stuck.

Vebjorn
  • 199

1 Answers1

1

So I think I figured out a way. You can use the vis-viva eq.:

$$v^2=\mu(\frac{2}{r}-\frac{1}{a})$$

Here is how you do it:

  1. Use it to find the circular velocity: for a circular orbit we have $a=r$ and we get: $v_c=\sqrt{\frac{\mu}{r_p}}$

  2. Find the velocity at perigee: $v_p=v_c+\Delta v$.

  3. Find $a$ by using the equation $v_p^2=\mu(\frac{2}{r_p }-\frac{1}{a})$. Solving for $a$ we get: $$a=\frac{1}{\left(\frac{2}{r_p}-\frac{v_p^2}{\mu}\right)}$$

  4. Find the radii $r_a$ at apogee: $a=\frac{r_p+r_a}{2}$. If we re-arrange we find that $r_a=2a-r_p$.

  5. Use the vis-viva eq. to calculate the velocity $v_a$: $$v_a=\sqrt{\mu\left(\frac{2}{r_a}-\frac{1}{a} \right)} $$

We can then put all of this together to obtain one formula. Firstly, note that $\frac{1}{a}=\frac{2}{r_p}-\frac{v_p^2}{\mu}$. If we substitute that in and multiply in the $\mu$ factor, we get:

$$v_a=\sqrt{\frac{2\mu}{r_a}-\frac{2\mu}{r_p}+v_p^2}$$

Now we try to express $r_a$: $r_a=2a-r_p=\frac{4}{r_p}-2\frac{v_p^2}{\mu}-r_p$. If we substitute this in:

$$v_a=\sqrt{\frac{2\mu}{\frac{4}{r_p}-2\frac{v_p^2}{\mu}-r_p}-\frac{2\mu}{r_p}+v_p^2}=\sqrt{\frac{2\mu^2 r_p}{4\mu-2v_p^2r_p-r_p^2\mu}-\frac{2\mu}{r_p}+v_p^2}$$

and then we have an expression for $v_a$. If we substitute $v_p$ with $v_p=v_c+\Delta v=\sqrt{\frac{\mu}{r_p}}+\Delta v$, we get an expression for $v_a$ only in terms of $r_p$ and $\Delta v$ (and $\mu$).

Edit: Here is an easier approach (as suggested by PM 2Ring):

Once you have found $r_a$ you can use conservation of angular momentum: $|\vec{L}|=|\vec{r}\times\vec{v}|=r\cdot v$ (it becomes a regular scalar multiplication since $\vec{r}$ and $\vec{v}$ are perpendicular, and $\sin 90^\circ=1$). Starting from $|\vec{L}|=r_a v_a = r_p v_p$ we get:

$$v_a=\frac{r_p\cdot v_p}{r_a}=\frac{r_p\cdot v_p}{2a-r_p}=\frac{r_p\cdot v_p}{\frac{2}{\left(\frac{2}{r_p}-\frac{v_p^2}{\mu}\right)}-r_p}= \frac{r_p\cdot v_p}{\frac{2r_p\mu}{2\mu-v_p^2r_p}-r_p}= \frac{r_p\cdot v_p(2\mu-v_p^2r_p)}{2r_p\mu-r_p(2\mu-v_p^2r_p)}$$

$$=\frac{r_p\cdot v_p(2\mu-v_p^2r_p)}{v_p^2r_p^2}= \frac{(2\mu-v_p^2r_p)}{v_p r_p}=\frac{2\mu}{v_p r_p}-v_p$$

So we get the much more simpler expression: $v_a=\frac{2\mu}{v_p r_p}-v_p$.

Vebjorn
  • 199