Lindblad operators seemingly not working as jump operators

Question

I am currently trying to understand the Lindblad superoperator $$\mathcal{L}[d]\rho = d \rho d^\dagger - (d^\dagger d \rho + \rho d^\dagger d)/2$$ for a simple 2 level system.

In the literature i found, the operator d is seen as a jump operator that can be written in the form $$d = \left|a\right>\left<b\right|.$$

Modeling a system with Hamiltonian $H=0$ (Markov Approximation) and one damping operator we get the Lindblad Master equation $$\dot{\rho} = \gamma \mathcal{L}[d]\rho$$ where $\gamma$ is the damping rate.

For example, with $d=\left| 0 \right>\left<1\right|$ the system will get pulled from $\left| 1 \right>$ to $\left|0 \right>$, just like i would expect when viewing $d$ as a jump operator.

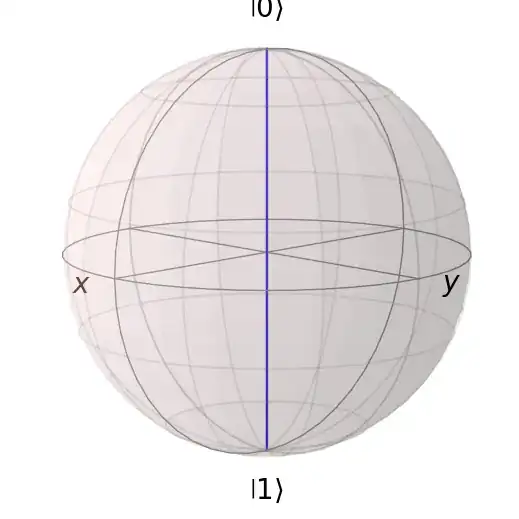
This is no longer the case when using $d = \left( \frac{\left| 0 \right> +\left| 1\right>}{\sqrt{2}} \right) \left< 0 \right|$. I would expect that the system is pulled from $\left| 0 \right>$ to $\frac{\left| 0 \right> +\left| 1\right>}{\sqrt{2}}$. The system will instead get damped towards $\left|1\right>$.

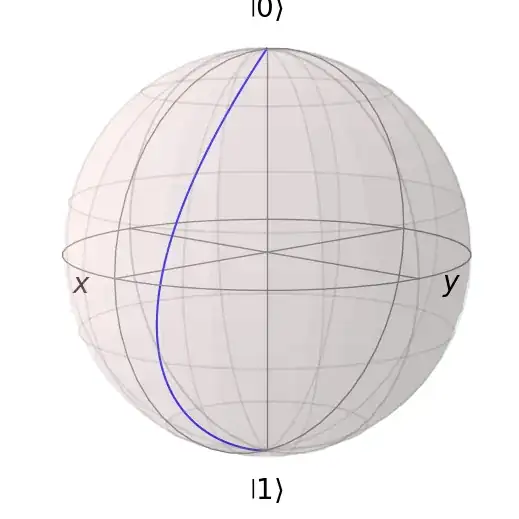
What is going here? Is this view of d as a jump operator only true for basis states? And if so, why? I have read here, that there are not formal constraints on the form of $d$, so how can an operator like $d = \left( \frac{\left| 0\right> +\left| 1\right>}{\sqrt{2}} \right) \left< 0\right|$ be interpretated?

Thank you for your help.

Answer 1

The issue is indeed in the non-orthogonality of the states you are using to create the jump operator. You can still create it and the Lindbladian is well-defined, but then you cannot adopt the standard interpretation of a jump operator inducing a transition between two energy levels anymore.

At the end of the day the only thing that matters is the spectral analysis of the Lindbladian, i.e., its eigenvectors and eigenvalues, including the steady state with 0 eigenvalue. For example, take an orthonormal basis of vectors $\{|a\rangle,|b\rangle\}$ that are eigenvectors of some relevant observable (typically, the energy levels of the system Hamiltonian). Then, let's build a Lindblad master equation with a single jump operator $L=|a\rangle\langle b|$. We observe: $$ L |a\rangle= 0,\quad L |b\rangle= |a\rangle,\quad L^\dagger L=|b\rangle\langle b|. $$ Which implies, $\mathcal{L}[|a\rangle\langle a|]=0$, $\mathcal{L}[|b\rangle\langle b|]=|a\rangle\langle a|-|b\rangle\langle b|$, $\mathcal{L}[|b\rangle\langle a|]=-0.5|b\rangle\langle a|$. That is to say, $|a\rangle$ is a steady state of the dynamics, and the state $|b\rangle$ will be driven towards $|a\rangle$ at infinite time. All the coherences will disappear.

Now let's analyze the Lindbladian you have written. As I said, you cannot interpret the jump operator $d=|+\rangle\langle 0|$ ($|+\rangle = \frac{|0\rangle +|1\rangle}{\sqrt{2}}$) as inducing transitions between these two states because of their lack of orthogonality. Indeed, the Lindbladian written with this jump operator acts as: $$ \mathcal{L}[|1\rangle\langle 1|]=0,\quad \mathcal{L}[|+\rangle\langle +|]=|1\rangle\langle 1|-|0\rangle\langle 0|,\quad \mathcal{L}[|0\rangle\langle 0|]=0.5(-|0\rangle\langle 0|+|1\rangle\langle 1|+|1\rangle\langle 0|+|0\rangle\langle 1|),\\ \mathcal{L}[|0\rangle\langle 1|]=-0.5|0\rangle\langle 1|. $$ So the conclusion is the same, although the intermediate dynamics will be slightly different: the steady state is $|1\rangle$, any other state will be driven towards $|1\rangle$, and all the coherences in the canonical basis will disappear.