Force problem related to adhesive and bonding

Question

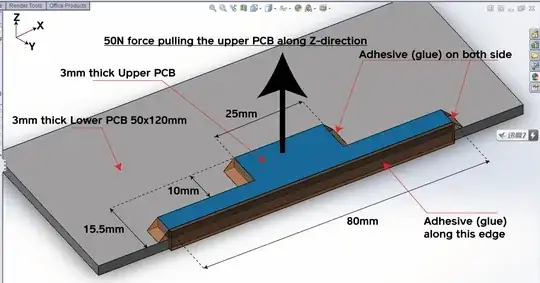
I have two PCBs (Printed Circuit Boards), and they are glued by adhesives, as shown in the pictures. The location of the adhesives is indicated in the picture (please notice that no adhesive is applied between the PCBs).

A $50 \ \text{N}$ force is applied on the upper PCB ($z$-direction). I use adhesive to prevent the PCB from being separated.

Here are the dimensions of the adhesives:

All the wedge-shaped adhesives have a height of $3 \ \text{mm}$ ($z$-direction) (the same as the PCBs), and the width is $1 \ \text{mm}$ ($x$-direction).

The long $80 \ \text{mm}$ adhesive is $1 \ \text{mm}$ thick ($y$-direction) and the height is $6 \ \text{mm}$ ($z$-direction).

I read from the adhesive specification sheet that the adhesive has the following properties:

$$\mathrm{tensile\: strength}: 22 \ \text{N/mm}^{2}$$

$$\mathrm{shear\: strength}: 18 \ \text{N/mm}^{2}.$$

How can I judge whether the adhesive is strong enough? What kind of formula should I use?

I attempted to solve the problem like this:

Step 1:

$$ \text{Total area of glue contact on the blue board} = 2 \, (3(10) + 3(5.5)) + 80 \, (3) = 333 \ \text{mm}^{2}$$

$$\text{Force resisting detachment of the blue board (shear force only in this situation)} = 333 \, (18) = 5994 \ \text{N}.$$

Step 2:

$$\text{Total area of the 4 glue contacts on the grey (ground) board} = 2 \, (1(10) + 1(5.5)) = 31 \ \text{mm}^{2}$$

$$\text{Area of the glue contact at the edge of the grey board} = 80 \, (3)= 240 \ \text{mm}^{2}.$$

So: $$\text{Total force resisting the glue from being pulled out from the grey board (tensile + shear force in this situation)} = 31 \, (22) + 240 \, (18) = 5002 \ \text{N}.$$

Therefore, in $5002 \ \text{N}$, is required to pull the blue out?

Answer 1

The force being applied is a force of $50 \ \text{N}$ in a static direction along only one of the $3$-dimensional planes ($z$).

This means the force applied will test the tensile strength of the adhesive tape, which is $22 \ \text{N}$ for every square area of tape measuring $1 \ \text{mm}$ on each side. Assuming the $50 \ \text{N}$ force is applied evenly, each square millimetre area will be subject to $50 \ \text{N}$ but will break at $22 \ \text{N}$.

The only equation you need is: $$\begin{align} \text{tensile strength} &> \text{force applied} \implies \text{adhesive tape is strong enough} \\ \text{tensile strength} &< \text{force applied} \implies \text{the tape will break}. \end{align}$$

Answer 2

I guess you should just multiply the surface of the contact between adhesive and the part by the tensile strength or the shear strength to obtain the maximum force normal or tangential to the surface of contact, respectively, that the adhesive can withstand. It looks like your design is OK with a large margin for 50N load, but you should compare both the forces and the moments of forces - it is not quite clear where exactly the load is applied.

Answer 3

For preliminary stress evaluation, you have all the data you need (for better performance, you need to evaluate critical torques/moments since wedges will experience turning forces upon lift).

Total shear-stress area

$$2 \times 3 \ \text{mm} \times 10 \ \text{mm} + 2 \times 3 \ \text{mm} \times 5.5 \ \text{mm} + 80 \ \text{mm} \times 6 \ \text{mm} = 573 \ \text{mm}^2.$$

Two big, two small and the long one adhesives will all feel shear stress on PCB parts along $z$ coordinate. So, the total shear pressure that PCB blue board will experience is $50 \ \text{N}/573 \ \text{mm}^2=87~\text{kPa}$. According to the specification of your adhesives, it has a shear strength of $18 \ \text{N/mm}^2 = 18~\text{MPa}$. So, adhesives will experience just $87~\text{kPa}/18~\text{MPa} = \color {red}{0.5\%}$ of critical shear stress pressure, which they can hold at maximum before break. $\ \color {green} {\text{OK}}$

Total tensile-stress area

$$2 \times 1 \ \text{mm} \times 10 \ \text{mm} + 2 \times 1 \ \text{mm} \times 5.5 \ \text{mm} = 31~\text{mm}^2.$$

Two big and two small adhesives will experience tensile stress - about decoupling from grey PCB board. (Long adhesive will not experience tensile stress because pulling force is not a normal to the glued surface of adhesive but parallel to it. So it will experience just shear-stress). The total tensile pressure that the blue board will experience is $50 \ \text{N}/31 \ \text{mm}^2=1.6~\text{MPa}$. Since, according to the adhesive specification, they have $22~\text{N/mm}^2=22~\text{MPa}$ of tensile strength, the blue board will experience about $1.6~\text{MPa}/22~\text{MPa} = \color {red}{7.2\%}$ of critical tensile stress pressure, which it can handle at maximum. $\ \color {green} {\text{OK}}$

Despite the fact that blue board will experience tensile stress over one order of magnitude greater than shear stress, both pressure types are within acceptable range of adhesives specification. I would start to worry only in case some pressure type goes $\gt 50\%$ of what adhesive can handle, which is not the case here.